Coniques circonscrites et inscrites à un triangle
En géométrie du triangle, une conique circonscrite est une conique passant par les trois sommets du triangle[1] et une conique inscrite est une conique tangente aux côtés, éventuellement étendus[2].
Équations
On note a = BC, b = CA, c = AB les longueurs des côtés d'un triangle ABC.
En coordonnées trilinéaires relativement au triangle ABC, une conique circonscrite à ce triangle est l'ensemble des points M de coordonnées (x : y : z) vérifiant l'équation générale :
pour un point de coordonnées trilinéaires (u : v : w). Le conjugué isogonal d'un point M de la conique circonscrite, distinct de A, B, C, appartient à la droite d'équation trilinéaire :
Cette droite rencontre la conique circonscrite au triangle ABC en 0, 1 ou 2 points selon la nature de la conique (ellipse, parabole ou hyperbole).
Une conique inscrite (ou tritangente), donc tangente aux trois côtés du triangle, a pour équation trilinéaire générale :
Le centre de la conique circonscrite ci-dessus a pour coordonnées trilinéaires :
- .
Le centre de la conique inscrite ci-dessus a pour coordonnées trilinéaires :
- .
Coniques circonscrites
Ellipses circonscrites
Ellipse circonscrite de Steiner

L'ellipse circonscrite de Steiner d'un triangle est l'ellipse passant par les trois sommets du triangle et de centre le centre de gravité du triangle. Elle correspond à l'ellipse inscrite de Steiner du triangle anticomplémentaire.
Pour un triangle donné, elle est l'ellipse circonscrite d'aire minimale, et son aire est proportionnelle à celle du triangle[3] :
Hyperboles circonscrites équilatères
Le théorème de Brianchon-Poncelet établit qu'une hyperbole circonscrite à un triangle est équilatère si et seulement si elle passe également par l'orthocentre du triangle, et dans ce cas, son centre est sur le cercle d'Euler[4]; on parle parfois de faisceau de Poncelet en parlant de l'ensemble des hyperboles circonscrites au triangle passant par l'orthocentre[5],[6].

Par rapport au triangle ABC, on se place dans le repère d'origine O, la base de la hauteur issue de A, et les vecteurs unitaires orientés dans le sens de et respectivement. Dans ce repère, les coordonnées sont de la forme : A (0 ; a), B (b ; 0), C (c ; 0), l'orthocentre H (0 ; d), avec . On cherche donc la forme d'une conique passant par ces quatre points. Son équation sera de la forme
La conique passant par A, B, C et H, on a en particulier les relations :
D'où α + γ = 0 : la conique est une hyperbole équilatère.
Réciproquement, dans le même repère, une hyperbole équilatère passant par A, B et C aura une équation de la forme :
Les intersections de la conique avec l'axe (OA) correspondent à X = 0, soit :
On a donc deux cas : (0 ; a), soit le point A, et (0 ; -bc/a) = (0 ; d), soit l'orthocentre H. QED.
Hyperbole de Kiepert

L'hyperbole de Kiepert d'un triangle est la courbe contenant tous les points de Lemoine du triangle. Elle passe par son centre de gravité.
Hyperbole de Feuerbach

L'hyperbole de Feuerbach d'un triangle est l'hyperbole passant par les trois sommets du triangle et dont le centre de symétrie est le point de Feuerbach du triangle. Elle passe par ses points de Nagel et de Gergonne.
Hyperbole de Jeřábek

L'hyperbole de Jeřábek d'un triangle est le conjugué isogonal de la droite d'Euler du triangle.
Elle passe par le centre du cercle circonscrit, l'orthocentre, le point symédian et le point de Kosnita du triangle.
Elle porte le nom de Václav Jeřábek (en).
Coniques inscrites
Brianchon a établi que les coniques inscrites dans un triangle sont telles que les céviennes des points de contact sont concourantes en un point appelé depuis point de Brianchon (c'est un cas dégénéré du théorème de Brianchon). Ce point est encore l'isotomique du point « complémentaire » du centre de la conique.
Poncelet a établi que les foyers de la conique inscrite sont isogonaux. On peut ainsi construire la conique tri-tangente à partir de la seule donnée du centre ou du point de Brianchon ou d'un foyer.
Ellipses
Ellipse de Steiner

L'ellipse de Steiner d'un triangle est l'unique ellipse tangente à chacun des côtés en leur milieu. De toutes les ellipses inscrites, l'ellipse de Steiner est celle d'aire maximale.
Le centre de gravité du triangle de référence est à la fois le centre et le point de Brianchon de l'ellipse de Steiner.
L'ellipse de Steiner d'un triangle est l'ellipse circonscrite de Steiner de son triangle médian.
Ellipse de Mandart

L'ellipse de Mandart d'un triangle est l'unique ellipse tangente à chacun des côtés aux points de contact des cercles exinscrits (les sommets du triangle de Nagel) ; son point de Brianchon est donc le point de Nagel du triangle[7]. Elle porte le nom de H. Mandart, qui l'a étudiée dans deux articles de la fin du XIXe siècle[8],[9],[10].
Le centre de l'ellipse de Mandart est le mittenpunkt du triangle.
Ellipse de Brocard

L'ellipse de Brocard d'un triangle est l'unique ellipse tangente à chacun des côtés aux sommets de son triangle symédian (le triangle formé par les points d'intersection des côtés et des symédianes du triangle).
Ses foyers sont les points de Brocard du triangle, son centre est donc au point milieu de Brocard. Son point de Brianchon est le point de Lemoine.
Ellipse de Lemoine

L'ellipse de Lemoine d'un triangle est l'unique ellipse tangente dont les foyers sont le centre de gravité du triangle et son point de Lemoine. Son point de Brianchon est donc le point milieu entre ces deux points.
Paraboles
Une conique inscrite au triangle est une parabole si et seulement si
Son foyer a alors pour coordonnées trilinéaires a/x2 : b/y2 : c/z2 et appartient au cercle circonscrit au triangle de référence, tandis que l'orthocentre est sur la droite directrice. Formellement, la parabole sera alors exinscrite (elle est tangente aux prolongements de deux des côtés du triangle), cependant, on parle tout de même de parabole inscrite.
Paraboles tritangentes

Du triangle ABC, on considère un point F de son cercle circonscrit, distinct de A, B et C. Alors la parabole de foyer F et de directrice la droite de Steiner de F est tangente aux trois côtés (étendus) du triangle.
Parabole de Kiepert
À partir du triangle ABC, on construit trois triangles isocèles semblables A'BC, B'CA et C'AB. Les triangles ABC et A'B'C' sont homologiques par rapport à une droite. La parabole de Kiepert du triangle est l'enveloppe des axes des homologies. La directrice de la parabole est la droite d'Euler du triangle. Son foyer est le point X(110) dans la nomenclature de Kimberling (qui correspond au point de Feuerbach du triangle tangentiel au triangle de base) ; ce point étant sur le cercle circonscrit au triangle de base, la parabole de Kiepert est bien tritangente.
Parabole d'Yff
La parabole d'Yff passe par les sommets du triangle d'Yff, qui est le triangle cévian de l'ellipse circonscrite de Steiner du triangle.
Hyperboles équilatères inscrites
On connait un résultat sur les hyperboles équilatères inscrites dans le triangle : leur centre se trouve sur le cercle de Mention, cercle polaire du triangle ou cercle des hauteurs[11].
Coniques variables
Selon la forme du triangle, certaines coniques de l'équation donnée peuvent changer de nature : si le triangle est acutangle, ce sera une ellipse inscrite, mais s'il est obtusangle, elle deviendra une hyperbole dont une des branches est tangente en un point de contact et la deuxième passe par les deux autres.
Conique orthique
La conique d'un triangle est l'unique section conique passant par les sommets de son triangle orthique (les bases des hauteurs du triangle de référence). Son point de Brianchon est donc l'orthocentre du triangle. Son centre est au point de Lemoine.
-
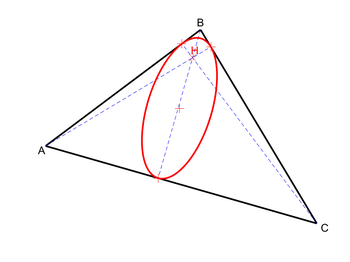 Pour un triangle acutangle, la conique orthique est une ellipse inscrite.
Pour un triangle acutangle, la conique orthique est une ellipse inscrite. -
 Pour un triangle obtusangle, la conique orthique est une hyperbole exinscrite.
Pour un triangle obtusangle, la conique orthique est une hyperbole exinscrite.
Conique de MacBeath
La conique de Serret (ou de MacBeath) est la conique inscrite de foyers le centre du cercle circonscrit et l'orthocentre du triangle. Son centre est le centre du cercle d'Euler, ses foyers sont le centre du cercle circonscrit et l'orthocentre du triangle, son point de Brianchon est le conjugué isotomique du centre du cercle circonscrit. Elle a d'abord été étudiée par Paul Serret, puis plus en profondeur par Macbeath[12].
Pour un triangle acutangle, la conique de MacBeath est une ellipse inscrite, aussi dénommée ellipse d'Euler[13]. Pour un triangle obtusangle, elle est une hyperbole exinscrite.
-
 Cas du triangle acutangle.
Cas du triangle acutangle. -
 Cas du triangle obtusangle.
Cas du triangle obtusangle.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Circumconic and inconic » (voir la liste des auteurs).
- ↑ (en) Eric W. Weisstein, « Circumconic », sur MathWorld
- ↑ (en) Eric W. Weisstein, « Inconic », sur MathWorld
- ↑ Georg Glaeser, Hellmuth Stachel et Boris Odehnal, The Universe of Conics : From the ancient Greeks to 21st century developments (lire en ligne)
- ↑ Brianchon et Poncelet, Géométrie des courbes. Recherches sur la détermination d'une hyperbole équilatère, au moyen de quatre conditions données, vol. 11 (1820-1821), 205-220 p. (lire en ligne)
- ↑ (en) Roger C. Alperin, « The Poncelet pencil of rectangular hyperbolas », Forum Geometricorum,, vol. 10, , p. 15-20 (lire en ligne)
- ↑ (en) Roger C. Alperin, « Reflections on Poncelet’s Pencil », Forum Geometricorum, vol. 15, , p. 93–98 (lire en ligne)
- ↑ Imre Juhász, « Control point based representation of inellipses of triangles », Annales Mathematicae et Informaticae, vol. 40, , p. 37–46 (MR 3005114, lire en ligne).
- ↑ (en) Bernard Gibert, « Generalized Mandart conics », Forum Geometricorum, vol. 4, , p. 177–198 (lire en ligne).
- ↑ H. Mandart, « Sur l’hyperbole de Feuerbach », Mathesis, , p. 81–89
- ↑ H. Mandart, « Sur une ellipse associée au triangle », Mathesis, , p. 241–245 (lire en ligne).
- ↑ J. Mention, « Sur l'hyperbole équilatère », Nouvelles annales de mathématiques : journal des candidats aux écoles polytechnique et normale, vol. 2, no 4, , p. 30-39 (lire en ligne)
- ↑ (en) Alexander Murray MacBeath, « A Compactness Theorem for Affine Equivalence-Classes of Convex Regions », Canadian Journal of Mathematics, vol. 3, , p. 54-61
- ↑ Patrice Debard, « Ellipse d'Euler », sur Geogebra.org (consulté le )
v · m | |
|---|---|
| Description | |
| Types | |
| Points remarquables (Nombre de Kimberling) | |
| Droites remarquables | |
| Cercles remarquables | |
| Triangles remarquables | |
| Courbes remarquables |
|
| Théorèmes |
|
| Relations entre triangles | |
| Résolution | |
 Portail de l’algèbre
Portail de l’algèbre































