Krzywa Béziera

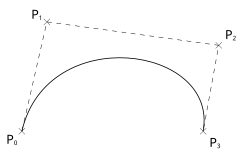
Krzywa Béziera (wym. ['be.zje.ra]) – parametryczna krzywa powszechnie stosowana w programach do projektowania inżynierskiego CAD (MicroStation), tworzenia grafiki wektorowej (Corel Draw, Adobe Illustrator, Inkscape), do reprezentowania kształtów znaków w czcionkach komputerowych (TrueType, METAFONT, Type1) i systemach przetwarzania grafiki (PostScript, MetaPost) oraz w grafice wektorowej (np. format SVG).

Krzywe Béziera zostały niezależnie opracowane przez Pierre’a Béziera^[1], francuskiego inżyniera firmy Renault, oraz Paula de Casteljau^[1], pracującego dla konkurencyjnej firmy Citroën. Prace nad krzywymi prowadzone były przez obu naukowców od początku lat 60. XX w., ale przez długi okres objęte ścisłą tajemnicą służbową. Dopiero pod koniec lat 60. pojawiły się pierwsze ogólnodostępne publikacje Pierre Béziera przedstawiające jego koncepcje, natomiast prace de Casteljau koncern Citroën ukrywał jeszcze przez kilka lat – pierwsze wzmianki o nim pojawiły się dopiero w 1971, gdy prace Béziera były znane od dawna. Do rozpowszechnienia się krzywych Béziera znacząco przyczynił się A.R. Forrest artykułem Interactive interpolation and approximation by Bezier polynomials opublikowanym w 1972 roku w branżowym piśmie „The Computer Journal”^[2].

Krzywe Béziera są krzywymi parametrycznymi, tzn. każda współrzędna punktu krzywej jest pewną funkcją liczby rzeczywistej będącej wspomnianym parametrem; aby określić krzywą na płaszczyźnie, potrzebne są dwie funkcje, aby określić krzywą w przestrzeni – trzy itd. Ze względu na rodzaj tych funkcji mówi się o krzywych wielomianowych oraz krzywych wymiernych. Powszechnie stosuje się również krzywe złożone z kawałków gładko połączonych krzywych wielomianowych bądź wymiernych, tzw. krzywych B-sklejanych (także: krzywych gładkich).

Niezależnie od rodzaju krzywej, na jej przebieg wpływa łamana kontrolna, określona za pomocą punktów kontrolnych, których liczba jest zwykle niewielka. Ta cecha bardzo ułatwia pracę interakcyjną, bowiem człowiek w naturalny sposób może ustalać położenie punktów i łatwo korygować błędy.

Podstawowe wiadomości

• Krzywe wielomianowe są powszechnie stosowane. W praktyce wykorzystuje się krzywe niskich stopni, opisywane niewielką liczbą punktów kontrolnych. Najpowszechniej stosowane są krzywe drugiego stopnia (trzy punkty kontrolne, np. fonty TrueType) lub trzeciego (cztery punkty kontrolne, np. fonty Type1, METAFONT, SVG, cała gama różnych pakietów graficznych); rzadziej stosuje się krzywe wyższych stopni. Krzywe wielomianowe są również dostępne w wielu bibliotekach programistycznych, np. OpenGL, Java2D, Tcl. Krzywe niskich stopni są wygodniejsze w użyciu, łatwiejsze w realizacji są różne algorytmy związane z takimi krzywymi np. obcinanie, wyznaczanie przecięć z innymi krzywymi, wyznaczanie ekstremów itp.
• Krzywe wymierne mają nad krzywymi wielomianowymi jedną zasadniczą przewagę: można za ich pomocą reprezentować wszystkie krzywe stożkowe, w szczególności okręgi, elipsy i ich wycinki, co ma fundamentalne znaczenie w projektowaniu wspomaganym komputerowo. Krzywe wielomianowe mogą okręgi i elipsy zaledwie aproksymować, co jednak nie jest wadą w zastosowaniach rysunkowych, gdzie dokładność nie jest priorytetem.

Zarówno krzywe wielomianowe, jak i wymierne cechuje jedna wspólną niedogodność – trudno za pomocą jednej krzywej przedstawiać skomplikowane kształty. Można co prawda dodawać nowe punkty kontrolne, ale to powoduje, że kontrola kształtu jest mocno utrudniona, przemieszczenie bowiem jednego punktu wpływa na całą krzywą, a ponadto im wyższy stopień, tym zmiana położenia punktów kontrolnych jest mniej widoczna (mówiąc obrazowo, trzeba punkty przemieszczać na duże odległości, aby odniosło to jakiś widoczny skutek). Z tego względu powszechnie stosuje się krzywe B-sklejane, które oferują lokalną kontrolę kształtu – na skutek przemieszczenia jednego punktu kontrolnego zmianie ulegnie tylko jego bliskie otoczenie. Krzywe B-sklejane są to takie krzywe, które składają się z fragmentów krzywych bądź to wielomianowych, bądź wymiernych (względnie niskiego stopnia), natomiast matematyczne równania opisujące taką krzywą gwarantują, iż w punktach połączenia różnych fragmentów krzywa będzie gładka. Szczególną popularność zyskały wymierne krzywe oraz powierzchnie B-sklejane, znane jako NURBS.

Podstawy matematyczne

Krzywe wielomianowe

• kod programu rysującego dowolne krzywe wielomianowe

Dane są punkty kontrolne ${\displaystyle p_{0},\dots ,p_{n}}$ w liczbie ${\displaystyle n+1.}$

Kształt krzywej Béziera opisują wielomiany, dla których przyjęto dziedzinę ${\displaystyle [0,1].}$ Stopień wielomianu wprost zależy od liczby punktów kontrolnych – wynosi ${\displaystyle n}$ (liczba punktów kontrolnych minus jeden). Wielomiany są zwykle przedstawiane w bazie wielomianów Bernsteina^[1] (oznaczane jako ${\displaystyle B_{i}^{n}(t),}$ bądź w literaturze anglojęzycznej ${\displaystyle B_{i,j}(t)}$). Wielomiany bazowe Bernsteina są wygodne w tym sensie, że punkty kontrolne są w naturalny sposób współczynnikami takiego wielomianu – nie trzeba dokonywać dodatkowych przeliczeń.

Dowolny punkt na krzywej jest opisywany zależnością:

${\displaystyle p(t)=\sum _{i=0}^{n}p_{i}B_{i}^{n}(t)\quad {\textrm {dla\ }}t\in [0,1],}$

np. krzywą dwuwymiarową opisuje para wielomianów:

${\displaystyle (x,y)=\left(\sum _{i=0}^{n}x_{i}B_{i}^{n}(t),\sum _{i=0}^{n}y_{i}B_{i}^{n}(t)\right).}$

Punkt ${\displaystyle p(t)}$ można również znaleźć za pomocą algorytmu de Casteljau.

Cechy charakterystyczne wielomianowych krzywych Béziera:

• Krzywa interpoluje skrajne punkty kontrolne (tj. ${\displaystyle p(0)=p_{0}}$ i ${\displaystyle p(1)=p_{n}}$), a przybliża pozostałe.
• Krzywa ma własność otoczki wypukłej, tzn. dla ${\displaystyle t\in [0,1]}$ punkt ${\displaystyle p(t)}$ leży w otoczce wypukłej punktów kontrolnych ${\displaystyle p_{0},\dots ,p_{n}}$^[3].
• Konstrukcja krzywej jest niezmiennicza względem przekształceń afinicznych, tzn. krzywa wyznaczona z przekształconych punktów kontrolnych jest taka sama jak krzywa po tym przekształceniu.
• Pojedyncza krzywa ma nieskończenie wiele reprezentacji – dla krzywej opisywanej przez ${\displaystyle n}$ punktów kontrolnych można wskazać taki ciąg punktów kontrolnych w liczbie ${\displaystyle n+k}$ ${\displaystyle (k=1,\dots ),}$ które opisują dokładnie tę samą krzywą. Taka procedura wyznaczania dodatkowych punktów nosi nazwę podnoszenia stopnia (ang. degree elevation). W praktyce stosuje się jednak krzywe możliwie niskich stopni, natomiast zwiększanie ilości punktów kontrolnych służy do konwersji między różnymi krzywymi.

Wadą wielomianowych krzywych Béziera jest to, że nie można za ich pomocą reprezentować krzywych stożkowych, okręgów, elips itd. Tej wady pozbawione są wymierne krzywe Béziera.

Wielomianowe krzywe Béziera trzeciego stopnia

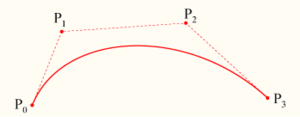
Najczęściej używane są krzywe trzeciego stopnia leżące na płaszczyźnie. Definiując krzywą trzeciego stopnia, określa się 4 punkty ${\displaystyle A,}$ ${\displaystyle B,}$ ${\displaystyle C}$ i ${\displaystyle D}$ (na rysunku odpowiednio ${\displaystyle P_{0},P_{1},P_{2},P_{3}}$), których położenie wyznacza przebieg krzywej. Krzywa ma swój początek w punkcie ${\displaystyle A}$ i skierowana jest w stronę punktu ${\displaystyle B.}$ Następnie zmierza w stronę punktu ${\displaystyle D}$, dochodząc do niego od strony punktu ${\displaystyle C.}$ Odcinek ${\displaystyle {\overline {AB}}}$ jest styczny do krzywej w punkcie ${\displaystyle A,}$ natomiast odcinek ${\displaystyle {\overline {CD}}}$ jest styczny w punkcie ${\displaystyle D}$

Krzywą Béziera trzeciego stopnia określa następujące równanie:

${\displaystyle P(t)=A(1-t)^{3}+3Bt(1-t)^{2}+3Ct^{2}(1-t)+Dt^{3}\quad {}}$ dla ${\displaystyle 0\leqslant t\leqslant 1,}$

czyli:

${\displaystyle P_{x}(t)=A_{x}(1-t)^{3}+3B_{x}t(1-t)^{2}+3C_{x}t^{2}(1-t)+D_{x}t^{3},}$

${\displaystyle P_{y}(t)=A_{y}(1-t)^{3}+3B_{y}t(1-t)^{2}+3C_{y}t^{2}(1-t)+D_{y}t^{3}.}$

Alternatywny zapis macierzowy:

${\displaystyle P(t)=\left[A,B,C,D\right]\cdot \left[{\begin{matrix}-1&3&-3&1\\3&-6&3&0\\-3&3&0&0\\1&0&0&0\end{matrix}}\right]\cdot \left[{\begin{matrix}t^{3}\\t^{2}\\t\\1\end{matrix}}\right].}$

Krzywa ma swój początek w punkcie ${\displaystyle A}$ ${\displaystyle (t=0)}$ i koniec w punkcie ${\displaystyle D}$ ${\displaystyle (t=1).}$

Krzywą Béziera trzeciego stopnia można też opisać następującym układem równań dla ${\displaystyle A=(x_{0},y_{0}),B=(x_{1},y_{1}),C=(x_{2},y_{2}),D=(x_{3},y_{3}){:}}$

${\displaystyle x_{(t)}=a_{x}t^{3}+b_{x}t^{2}+c_{x}t+x_{0},}$

${\displaystyle x_{1}=x_{0}+{\frac {c_{x}}{3}},}$

${\displaystyle x_{2}=x_{1}+{\frac {c_{x}+b_{x}}{3}},}$

${\displaystyle x_{3}=x_{0}+c_{x}+b_{x}+a_{x},}$

${\displaystyle y_{(t)}=a_{y}t^{3}+b_{y}t^{2}+c_{y}t+y_{0},}$

${\displaystyle y_{1}=y_{0}+{\frac {c_{y}}{3}},}$

${\displaystyle y_{2}=y_{1}+{\frac {c_{y}+b_{y}}{3}},}$

${\displaystyle y_{3}=y_{0}+c_{y}+b_{y}+a_{y}.}$

Zdefiniowane w ten sposób wzory mogą zostać odwrócone tak, by otrzymać zmienne kierunkowe (są one stałe dla każdej krzywej Béziera):

${\displaystyle c_{x}=3(x_{1}-x_{0}),}$

${\displaystyle b_{x}=3(x_{2}-x_{1})-c_{x},}$

${\displaystyle a_{x}=x_{3}-x_{0}-c_{x}-b_{x},}$

${\displaystyle c_{y}=3(y_{1}-y_{0}),}$

${\displaystyle b_{y}=3(y_{2}-y_{1})-c_{y},}$

${\displaystyle a_{y}=y_{3}-y_{0}-c_{y}-b_{y}.}$

Wymierne krzywe Béziera

 Osobny artykuł: Wymierna krzywa Béziera.

Wymierna krzywa Béziera to rzut środkowy wielomianowej krzywej Béziera zdefiniowanej we współrzędnych jednorodnych na płaszczyznę ${\displaystyle W=1.}$ Tak samo dane jest ${\displaystyle n+1}$ punktów kontrolnych.

Jeśli przestrzeń jednorodna jest ${\displaystyle k+1}$-wymiarowa, wówczas do opisu krzywej potrzebne jest tyleż wielomianów. Dowolny punkt krzywej wielomianowej jest dany jako ${\displaystyle P(t)=(X(t),Y(t),\dots ,W(t)).}$ Po przejściu na współrzędne kartezjańskie (rzucie środkowym ${\displaystyle P(t)}$ na płaszczyznę ${\displaystyle W=1}$) otrzymuje się ${\displaystyle k}$ wyrażeń wymiernych, a punkt na tej płaszczyźnie dany jest wzorem ${\displaystyle p(t)=\left({\frac {X(t)}{W(t)}},{\frac {Y(t)}{W(t)}},\dots \right).}$

Jeśli ${\displaystyle W(t)={\textrm {const}}}$ to krzywa jest wielomianowa – mówiąc nieformalnie krzywe wielomianowe to specjalny przypadek krzywych wymiernych.

Dowolny punkt na krzywej wymiernej dany jest wzorem:

${\displaystyle p(t)={\frac {\sum _{i=0}^{n}w_{i}p_{i}B_{i}^{n}(t)}{\sum _{i=0}^{n}w_{i}B_{i}^{n}(t)}}\qquad t\in [0,1],}$

gdzie ${\displaystyle w_{i}}$ to współrzędna W, jednak częściej nazywana jest wagą punktu kontrolnego.

Aby wyznaczyć punkt na krzywej, można także posłużyć się algorytmem de Casteljau albo wariantem dla krzywych wymiernych lub wielomianowych.

Atuty w stosunku do wielomianowych krzywych Béziera są następujące:

• mogą reprezentować wszystkie krzywe stożkowe, co ma znaczenie w zastosowaniach CAD;
• rzut perspektywiczny krzywej wymiernej jest zawsze krzywą wymierną, podczas gdy rzut perspektywiczny krzywej wielomianowej nie musi być krzywą wielomianową, co ma znaczenie w grafice komputerowej;
• wagi ${\displaystyle w_{i}}$ pozwalają na lepszą kontrolę nad kształtem krzywej.

Krzywe B-sklejane

 Osobny artykuł: Krzywa B-sklejana.

Krzywe B-sklejane składają się z fragmentów wielomianowych bądź wymiernych krzywych Béziera, najczęściej niskiego stopnia ${\displaystyle (n).}$ Dla krzywej B-sklejanej parametr ${\displaystyle t}$ również należy do przedziału ${\displaystyle [0,1].}$ Przedział ten jest dzielony na podprzedziały, a liczby określające ich granicę nazywane są węzłami (ang. knot). Kolejne węzły mogą być sobie równe, tworząc w ten sposób puste podprzedziały – nie jest to błąd.

Jeśli węzłów jest ${\displaystyle m+1}$ ${\displaystyle (u_{0},\dots ,u_{m}),}$ a stopień wielomianów jest równy ${\displaystyle n,}$ to do określenia krzywej potrzebne jest ${\displaystyle m-n}$ punktów kontrolnych, zaś liczba krzywych, które składają się na całość, wynosi ${\displaystyle m-2n.}$ Sklejane krzywe są zdefiniowane na przedziale ${\displaystyle [u_{n},u_{m-n}],}$ nie na ${\displaystyle [0,1].}$

Dowolny punkt na krzywej B-sklejanej jest dany wzorem, który wynika z algorytmu Mansfielda-de Boora-Coxa:

${\displaystyle p(t)=\sum _{i=0}^{m-n-1}p_{i}N_{i}^{n}(t)\quad {\textrm {dla\ }}t\in [u_{n},u_{m-n}],}$

gdzie ${\displaystyle N_{i}^{n}}$ to unormowane funkcje B-sklejane stopnia ${\displaystyle n.}$

Krzywe B-sklejane mają następujące zalety w stosunku do krzywych wielomianowych i wymiernych:

• Lokalna kontrola kształtu – przemieszczanie jednego punktu kontrolnego wpływa na niewielkie otoczenie tego punktu, najwyżej ${\displaystyle n}$ sąsiednich krzywych.
• Możliwość dowolnego rozmieszczania węzłów daje lepszą i większą kontrolę nad kształtem krzywej. Dodatkowo jeśli węzły pokrywają się, tzn. istnieją puste podprzedziały, uzyskuje się „ostre” (nie gładkie) połączenia.
• W łatwy sposób można wstawiać nowe węzły (ang. knot insertion), dzięki czemu proces modelowania jest prostszy.

Szczególne znaczenie i popularność zyskały wymierne krzywe B-sklejane (NURBS), łączące zalety zwykłych krzywych wymiernych z wymienionymi wyżej.

Zobacz też

• lista krzywych
• płaty Béziera

Przypisy

Bibliografia

• James DJ.D. Foley James DJ.D. i inni, Wprowadzenie do grafiki komputerowej, JanJ. Zabrodzki (tłum.), Warszawa: Wydawnictwa Naukowo-Techniczne, 1995, ISBN 83-204-1840-2 .brak strony (książka)
• MichałM. Jankowski MichałM., Elementy grafiki komputerowej, Warszawa: Wydawnictwa Naukowo-Techniczne, 1990, ISBN 83-204-1326-5 .
• PrzemysławP. Kiciak PrzemysławP., Podstawy modelowania krzywych i powierzchni: zastosowania w grafice komputerowej, Warszawa: Wydawnictwa Naukowo-Techniczne, 2000, ISBN 83-204-2464-X .brak strony (książka)

Linki zewnętrzne

• Interaktywny applet Javy obrazujący krzywe Béziera