Elipsa

Ten artykuł dotyczy figury geometrycznej. Zobacz też: inne znaczenia tego słowa.

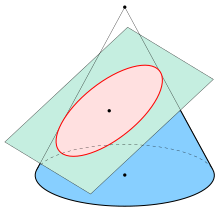
Elipsa (gr. ἔλλειψις, elleipsis – „brak, opuszczenie, pominięcie”^[1][2], zob. geneza) – przypadek ograniczonej krzywej stożkowej, czyli krzywej będącej częścią wspólną powierzchni stożkowej oraz przecinającej ją płaszczyzny. Elipsę można zdefiniować także jako miejsce geometryczne tych wszystkich punktów płaszczyzny, dla których suma odległości od dwóch ustalonych punktów jest stałą^[3].

Elipsy powstają jako obrazy okręgu lub sfery w rzucie równoległym i pewnych przypadkach rzutu perspektywicznego. Okręgi są szczególnymi przypadkami elips. Elipsa jest domkniętym i ograniczonym przypadkiem krzywej stopnia drugiego danej wzorem uwikłanym lub krzywej wymiernej drugiego stopnia. Jest najprostszą figurą Lissajous powstającą, gdy drgania poziome i pionowe mają tę samą częstotliwość.

Elipsa jest krzywą gładką, zamkniętą, symetryczną względem jej środka.

Podstawowe pojęcia i własności

Oś wielka i oś mała

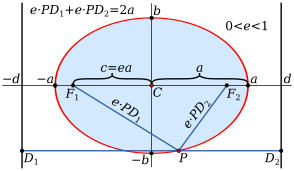
Odległość między punktami antypodycznymi elipsy, czyli parami punktów, których środek odcinka wyznaczany przez te punkty jest zarazem środkiem symetrii elipsy, jest maksymalna i minimalna wzdłuż dwóch prostopadłych kierunków – osi wielkiej (średnicy transwersalnej) oraz osi małej (średnicy sprzężonej).

Półoś wielka, półoś mała

Niech ${\displaystyle a}$ i ${\displaystyle b}$ oznaczają półoś wielką oraz półoś małą elipsy, tj. połowy odpowiednio osi wielkiej i małej.

Ogniska

Ogniskami elipsy ${\displaystyle F_{1}}$ oraz ${\displaystyle F_{2}}$ nazywamy punkty na osi wielkiej, takie że suma odległości dowolnego punktu elipsy od tych punktów jest stała, równa długości osi wielkiej ${\displaystyle 2a.}$

Półogniskowa, ogniskowa

Półogniskową ${\displaystyle c}$ nazywamy odległości ognisk od środka elipsy:

${\displaystyle c={\sqrt {a^{2}-b^{2}}}.}$

Jeżeli ${\displaystyle a}$ jest równe ${\displaystyle b,}$ to ogniska pokrywają się ze środkiem i wówczas elipsa staje się okręgiem o promieniu ${\displaystyle r=a=b.}$

Ogniskową elipsy nazywa się odległość ognisk od siebie; jest ona równa 2c.

Kierownice

Kierownice elipsy to proste prostopadłe do półosi wielkiej elipsy; są odległe od środka elipsy o

${\displaystyle d={\frac {a^{2}}{c}}}$

Dla okręgu ${\displaystyle (c=0)}$ kierownice znajdują się „w nieskończoności”.

Mimośród

Mimośrodem elipsy (ekscentrycznością elipsy) nazywa się liczbę ${\displaystyle e,}$ równą ilorazowi długości półogniskowej ${\displaystyle c}$ do długości półosi wielkiej ${\displaystyle a,}$ tj.

${\displaystyle e={\frac {c}{a}}.}$

Mimośród zawiera się w przedziale od 0 do 1. Jest on równy zeru, gdy ${\displaystyle a=b,}$ tj. gdy elipsa redukuje się do okręgu. Gdy elipsa wydłuża się, to współczynnik ${\displaystyle {\tfrac {a}{b}}}$ dąży do nieskończoności; wtedy mimośród dąży do 1.

Odległość ${\displaystyle ae}$ od ogniska do środka nazywana jest mimośrodem liniowym (ekscentrycznością liniową) elipsy.

W obliczeniach geodezyjnych i kartograficznych mają zastosowanie następujące oznaczenia^[4]:

mimośród	${\displaystyle e}$	${\displaystyle e^{2}={\frac {a^{2}-b^{2}}{a^{2}}}}$
drugi mimośród	${\displaystyle e'}$	${\displaystyle {e'}^{2}={\frac {a^{2}-b^{2}}{b^{2}}}}$
trzeci mimośród	${\displaystyle e''}$	${\displaystyle {e''}^{2}=m={\frac {a-b}{a+b}}}$

Parametry te mają zastosowanie do elipsoidy obrotowej, ale wywodzą się z elipsy południkowej.

Spłaszczenie

Podobnie w obliczeniach geodezyjnych i astronomicznych są używane parametry elipsy nazywane spłaszczeniem:

(pierwsze) spłaszczenie	${\displaystyle f={\frac {a-b}{a}}}$	Podstawowe, odwrotność 1/f służy do określenia elipsoidy odniesienia.
drugie spłaszczenie	${\displaystyle f'={\frac {a-b}{b}}}$	Rzadziej używane.
trzecie spłaszczenie	${\displaystyle n=f''={\frac {a-b}{a+b}}}$	Używane w obliczeniach geodezyjnych.

Geneza nazwy

Nazwa „elipsa” została zaczerpnięta (według Pappusa z Aleksandrii) przez Apoloniusza z Pergi z wczesnej pitagorejskiej terminologii dotyczącej przykładania pól powierzchni: po przyłożeniu prostokąta do odcinka (tj. umieszczeniu podstawy prostokąta wzdłuż odcinka tak, by jeden z końców odcinka i jeden z końców podstawy pokrywały się) przyłożonemu prostokątowi „brakowało” do długości odcinka; równanie elipsy to ${\displaystyle y^{2}=lx\pm b^{2}x^{2}/a^{2},}$ gdzie ${\displaystyle l=b^{2}/a,}$ skąd ${\displaystyle y^{2}<lx,}$ a więc kwadrat rzędnej punktu elipsy jest mniejszy niż pole prostokąta o bokach długości równych parametrowi ${\displaystyle l}$ oraz odciętej.

Ślad tej relacji można też zaobserwować w równaniu ogólnym krzywej stożkowej:

${\displaystyle ax^{2}+2hxy+bx^{2}+2gx+2fy+c=0,}$

gdzie ${\displaystyle a,b,c,f,g,h}$ – parametry krzywej.

Dla elipsy spełniona jest nierówność ${\displaystyle h^{2}<ab.}$

Kreślenie elipsy

Metoda szpilek i sznurka

Elipsę można nakreślić za pomocą dwóch szpilek (pinezek), kawałka sznurka i rysika (ołówka, długopisu):

Należy wetknąć szpilki w dwa punkty papieru, które staną się ogniskami elipsy, następnie zawiązać sznurek w luźną pętlę wokół szpilek, po czym naciągnąć sznurek za pomocą rysika tak, by powstał trójkąt. Elipsa zostanie nakreślona poprzez przesuwanie rysika po powierzchni kartki przy zachowaniu napięcia sznurka.

Aby nakreślić elipsę wpisaną w dany prostokąt, styczną do jego czterech boków w ich środkach, należy najpierw określić położenie ognisk i długość pętli:

Niech ${\displaystyle A,B,C,D}$ będą wierzchołkami prostokąta danymi w porządku odwrotnym do wskazówek zegara, gdzie ${\displaystyle AB}$ jest jednym z dłuższych boków. Należy nakreślić okrąg o środku w ${\displaystyle A}$ i promieniu równym długości krótszego boku ${\displaystyle AD,}$ a następnie wyznaczyć styczną do okręgu przechodzącą przez ${\displaystyle B.}$ Długość ${\displaystyle L}$ odcinka od ${\displaystyle B}$ do punktu styczności jest odległością między ogniskami. Należy następnie nakreślić dwie proste prostopadłe przez środek prostokąta równoległe do jego boków; będą to osie wielka i mała elipsy. Ogniska rozmieszczone są symetrycznie na osi wielkiej w odległości ${\displaystyle {\tfrac {L}{2}}}$ od środka.

Aby dostosować długość pętli sznurka należy wetknąć szpilkę w jedno z ognisk, drugą zaś w przeciwny (położony dalej) koniec osi głównej, po czym wykonać ścisłą pętlę wokół dwóch szpilek (tak, by była napięta). Oznacza to, że długość sznurka jest określona wzorem ${\displaystyle k_{k}=2c+2a,}$ gdzie ${\displaystyle 2c}$ jest długością ogniskowej^[a], a ${\displaystyle 2a}$ to długość osi wielkiej.

Metoda cyrkla i linijki

Elipsa może być także nakreślona za pomocą linijki, ekierki oraz rysika:

Należy nakreślić dwie proste prostopadłe ${\displaystyle M,N}$ na papierze; będą to osie wielka i mała elipsy. Następnie na linijce należy oznaczyć punkty ${\displaystyle A,B,C.}$ Obracając jedną ręką linijkę tak, by punkt ${\displaystyle A}$ zawsze leżał na prostej ${\displaystyle M,}$ a punkt ${\displaystyle B}$ na prostej ${\displaystyle N}$ i kreśląc rysikiem za pomocą drugiej ręki na papierze, śladem punktu ${\displaystyle C}$ na linijce otrzymuje się elipsę.

Metoda ta może być wykorzystana przy cięciu elips z materiałów drewnianych za pomocą frezarek (ręcznych). Innymi przyrządami korzystającymi z tej zasady są elipsograf i cyrkiel drążkowy: linijka zastąpiona jest prętem z uchwytem na rysik (punkt ${\displaystyle C}$) z jednej strony oraz dwoma przesuwnymi bolcami, które przesuwają się w dwóch prostopadłych prowadnicach wyciętych w płycie.

Równania analityczne elipsy

(1) W układzie współrzędnych kartezjańskim ${\displaystyle (x,y)}$ elipsa mająca środek w początku układu współrzędnych, o osi wielkiej skierowanej wzdłuż osi ${\displaystyle OX,}$ dana jest równaniem analitycznym

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,}$

gdzie ${\displaystyle a}$ i ${\displaystyle b}$ są długościami półosi; ${\displaystyle a>b.}$

Wtedy ogniska mają współrzędne ${\displaystyle F_{1}=(-c,0)}$ i ${\displaystyle F_{2}=(c,0).}$

(2) W układzie współrzędnych biegunowych ${\displaystyle (r,\theta )}$ elipsę opisuje wzór

${\displaystyle r^{2}={\frac {b^{2}}{1-e^{2}\cos ^{2}\theta }}={\frac {a^{2}b^{2}}{a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta }},}$

gdzie ${\displaystyle e}$ jest mimośrodem.

(3) Elipsa dana jest też układem równań parametrycznych

${\displaystyle {\begin{cases}x=a\cos t,\\y=b\sin t,\end{cases}}}$

gdzie ${\displaystyle 0\leqslant t<2\pi }$ – parametr.

Postać parametryczna jest wygodna do a) kreślenia numerycznego elipsy b) obliczeń numerycznych, np. łuku elipsy.

Uwaga: Parametr ${\displaystyle t}$ nie ma sensu kąta ${\displaystyle \alpha }$ nachylenia promienia wodzącego punktów elipsy do osi ${\displaystyle OX,}$ jak to ma miejsce w równaniach parametrycznych okręgu. Jest to istotne przy obliczeniach łuku elipsy (patrz niżej); zachodzi jednak związek:

${\displaystyle tg(\alpha )={\frac {b}{a}}tg(t).}$

Własności

Pole elipsy

Pole powierzchni ograniczonej przez elipsę opisuje prosty wzór:

${\displaystyle S=\pi ab.}$

Obwód elipsy

– nie daje się w ogólnym przypadku zapisać w postaci algebraicznej.

(1) Wzory przybliżone na obwód elipsy

${\displaystyle \ell \approx \pi \left({\tfrac {3}{2}}(a+b)-{\sqrt {ab}}\right);}$

lepsze przybliżenie

${\displaystyle \ell \approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\;\right];}$

jeszcze lepsze przybliżenie

${\displaystyle \ell \approx \pi \left(a+b\right)\left(1+{\frac {3h}{10+{\sqrt {4-3h}}}}\right),}$

gdzie ${\displaystyle h=(a-b)^{2}/(a+b)^{2}.}$

2) Dokładny wzór na obwód elipsy wyraża się tzw. całką eliptyczną zupełną ${\displaystyle E}$ drugiego rodzaju

${\displaystyle \ell =4a\ E(e)=4a\int _{0}^{\frac {\pi }{2}}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta =4a\int _{0}^{1}{\frac {\sqrt {1-e^{2}t^{2}}}{\sqrt {1-t^{2}}}}\ dt,}$

gdzie ${\displaystyle e}$ – mimośród, ${\displaystyle a}$ – półoś wielka elipsy.

Np. dla ${\displaystyle a=2}$ oraz ${\displaystyle b=1}$ mimośród wynosi ${\displaystyle e=0{,}866025,}$ co daje w przybliżeniu obwód elipsy równy ${\displaystyle l=9{,}6884482.}$

Uwagi:

(1) Całki eliptyczne są stablicowane; są kalkulatory online całek eliptycznych.

(2) Istnieją różne konwencje zapisu funkcji ${\displaystyle E{:}}$ w niektórych argumentem jest kwadrat mimośrodu, nie sam mimośród; właściwy wzór pod znakiem całki wyrażonej przez mimośród ${\displaystyle e}$ będzie zawierał ${\displaystyle e}$ w drugiej potędze (nigdy w pierwszej czy czwartej).

Długość łuku elipsy

Długość łuku elipsy oblicza się za pomocą całki eliptycznej niezupełnej drugiego rodzaju^[5] („niezupełność” całki oznacza, że liczy się nie cały obwód, ale łuk w zadanym zakresie kątów.)

(a) Łuk elipsy o półosiach ${\displaystyle a,b,}$ ograniczony kątami ${\displaystyle \alpha _{1},\alpha _{2},}$ mierzonymi od osi ${\displaystyle OX}$ do punktów początkowego i końcowego łuku elipsy, jest zadany przez różnicę całek eliptycznych niezupełnych 2 rodzaju wzorem

${\displaystyle \ell (\alpha _{1},\alpha _{2})=a\,E(e,\psi _{2})-a\,E(e,\psi _{1}),}$

gdzie: ${\displaystyle \psi _{2}=arctg{\Big (}{\frac {a}{b}}tg(\alpha _{2}){\Big )},}$ ${\displaystyle e={\sqrt {1-(b/a)^{2}}}}$ – mimośród elipsy.

(wartości parametrów ${\displaystyle \psi _{1},\psi _{2},}$ którym odpowiadają katy ${\displaystyle \phi _{1},\phi _{2}}$ ograniczające łuk elipsy, wynikają z równań parametrycznych elipsy)

(b) Łuk elipsy o półosiach ${\displaystyle a,b,}$ ograniczony kątami ${\displaystyle \alpha _{1}=0,\alpha _{2},}$ mierzonymi od osi ${\displaystyle OX}$ do punktów początkowego i końcowego łuku elipsy, jest zadany przez całkę eliptyczną niezupełną 2 rodzaju wzorem

${\displaystyle \ell (\alpha _{1}=0,\alpha _{2})=a\,E(e,\psi _{2}),}$

gdzie ${\displaystyle \psi _{2}=arctg{\Big (}{\frac {a}{b}}tg(\alpha _{2}){\Big )}.}$

Styczna

Styczna w punkcie ${\displaystyle P}$ do elipsy o ogniskach ${\displaystyle F_{1},\ F_{2}}$ jest dwusieczną kąta zewnętrznego trójkąta ${\displaystyle \Delta F_{1}PF_{2}.}$ Jest to równoznaczne z tym, że promień świetlny wychodzący z jednego ogniska elipsy po odbiciu (zgodnie z zasadą, że kąt padania jest równy kątowi odbicia) od krawędzi elipsy przejdzie przez drugie ognisko (kolorowe kąty na rysunku 1 mają równe miary).

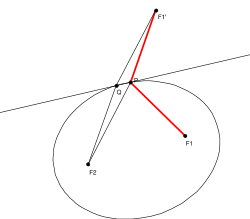
Dowód:

Załóżmy, że dwusieczna tego kąta nie jest styczną, czyli przecina elipsę w pewnym punkcie ${\displaystyle Q}$ różnym od ${\displaystyle P.}$

Niech ${\displaystyle F_{1}'}$ będzie odbiciem ${\displaystyle F_{1}}$ w dwusiecznej. Z symetrii wynika, że

${\displaystyle F_{1}P=F_{1}'P,}$ więc ${\displaystyle F_{2}P+PF_{1}'=2a,}$

gdzie ${\displaystyle a}$ oznacza długość dużej półosi elipsy. Podobnie pokazujemy, że

${\displaystyle F_{2}Q+QF_{1}'=2a.}$

Ponieważ kąt ${\displaystyle F_{1}PF_{1}'}$ jest kątem zewnętrznym trójkąta ${\displaystyle F_{1}PF_{2},}$ to punkty ${\displaystyle F_{1}',P,F_{2}}$ są współliniowe, więc ${\displaystyle F_{1}',Q,F_{2}}$ są niewspółliniowe.

Stąd ${\displaystyle F_{2}P+PF_{1}'<F_{2}Q+QF_{1}'.}$ Jest to sprzeczne z ${\displaystyle F_{2}P+PF_{1}'=2a=F_{2}Q+QF_{1}'.}$

Zakładając nieprawdziwość tezy, doszliśmy do sprzeczności, zatem teza została udowodniona.

Dwie styczne

Gdy z punktu ${\displaystyle S}$ leżącego na zewnątrz elipsy poprowadzimy dwie proste, styczne do elipsy w punktach ${\displaystyle K}$ i ${\displaystyle L,}$ to

${\displaystyle \angle KSF_{1}=\angle LSF_{2},}$

${\displaystyle \angle KF_{1}S=\angle LF_{1}S.}$

(kąty o tych samych kolorach na rysunku 2 mają równe miary).

Dowód pierwszej równości:

Odbijamy elipsę w obu stycznych. Ogniska obrazów oznaczamy odpowiednio przez ${\displaystyle F_{1}',\ F_{1}'',\ F_{2}',\ F_{2}''.}$

Pamiętając własność stycznej udowodnioną powyżej, łatwo otrzymujemy, że ${\displaystyle F_{2}F_{1}'=F_{2}F_{1}''=2a}$ (${\displaystyle a}$ – duża półoś). Oprócz tego, ${\displaystyle SF_{1}'=SF_{1}'',}$ bo są obrazami tego samego odcinka.

Zatem ${\displaystyle \Delta SF_{2}F_{1}'=\Delta SF_{2}F_{1}'',}$

więc ${\displaystyle \angle SF_{2}F_{1}'=\angle SF_{2}F_{1}''}$

oraz ${\displaystyle \angle F_{2}SF_{1}'=\angle F_{2}SF_{1}''.}$

${\displaystyle \angle F_{2}SF_{1}''=\angle KSL+\angle F_{1}''SL-\angle KSF_{2},}$

${\displaystyle \angle F_{2}SF_{1}'=\angle KSL'+\angle F_{2}SK-\angle L'SF_{1}',}$ gdzie ${\displaystyle L'}$ – odbicie ${\displaystyle L}$ w ${\displaystyle SK.}$

Lewe części tych równości są równe, oraz, ${\displaystyle \angle KSL=\angle KSL';}$ stąd ${\displaystyle \angle F_{2}SK-\angle L'SF_{1}'=\angle F_{1}''SL-\angle KSF_{2},}$

czyli ${\displaystyle 2\angle KSF_{2}=\angle F_{1}''SL+\angle L'SF_{1}'.}$

Ponieważ ${\displaystyle \angle L'SF_{1}'=\angle F_{1}''SL,}$

to ${\displaystyle \angle KSF_{2}=\angle F_{1}''SL=\angle L'SF_{1}'=\angle LSF_{1}.}$

Więc mamy ${\displaystyle \angle KSF_{2}=\angle LSF_{1},}$ a stąd wynika równość ${\displaystyle \angle KSF_{1}=\angle LSF_{2},}$ którą trzeba było udowodnić.

Trójkąt opisany

Gdy punkty ${\displaystyle F_{1},\ F_{2}}$ leżące wewnątrz trójkąta ${\displaystyle ABC}$ spełniają

${\displaystyle \angle CBF_{1}=\angle ABF_{2},}$

${\displaystyle \angle BAF_{1}=\angle CAF_{2},}$

to istnieje elipsa o ogniskach ${\displaystyle F_{1},\ F_{2}}$ wpisana w trójkąt, czyli styczna do jego trzech boków (rys. 3). Wtedy zachodzi również ${\displaystyle \angle BCF_{1}=\angle ACF_{2}.}$ Szczególnym przypadkiem takiej elipsy jest elipsa o ogniskach w ortocentrum i środku okręgu opisanego na trójkącie.

Dowód:

Możemy tak dobrać dużą półoś elipsy, żeby była styczna do ${\displaystyle AB.}$ Z twierdzenia odwrotnego do powyższej własności o dwóch stycznych (które jest oczywistą konsekwencją tej własności) otrzymujemy, że jest ona styczna do pozostałych boków trójkąta, bo zachodzą równości odpowiednich kątów. Korzystając ponownie z własności stycznych, otrzymujemy równość ${\displaystyle \angle BCF_{1}=\angle ACF_{2}.}$

Dokonując rachunku na kątach, otrzymujemy powyższe równości dla ortocentrum i środka okręgu opisanego, z czego wynika, że istnieje elipsa wpisana w trójkąt o takich ogniskach.

Okrąg opisany

Niech ${\displaystyle X}$ będzie rzutem prostokątnym ogniska elipsy na styczną do niej. Miejscem geometrycznym wszystkich punktów ${\displaystyle X}$ jest okrąg o środku w środku odcinka łączącego ogniska i o promieniu równym dużej półosi elipsy (czerwony okrąg na rys. 4).

Dowód:

Poprowadźmy dwie równoległe styczne do elipsy w punktach ${\displaystyle X,\ Y.}$ Są one symetryczne względem środka ${\displaystyle S}$ elipsy, więc ${\displaystyle F_{1}XF_{2}Y}$ jest równoległobokiem.

Niech ${\displaystyle A,\ D}$ będą rzutami prostokątnymi ognisk ${\displaystyle F_{1},\ F_{2}}$ na styczną w ${\displaystyle Y,}$ zaś ${\displaystyle B,\ C}$ na styczną w ${\displaystyle X.}$ Odbijamy ${\displaystyle X}$ w prostej ${\displaystyle AB,}$ otrzymując punkt ${\displaystyle X'.}$

Punkty ${\displaystyle B,\ D}$ są symetryczne względem ${\displaystyle S,}$ więc ${\displaystyle BX'=BX=YD.}$

Stąd ${\displaystyle BDYX'}$ jest równoległobokiem, czyli ${\displaystyle BD=YX'.}$

Ale ${\displaystyle YX'=YF_{1}+F_{1}X'=YF_{1}+F_{1}X.}$

Więc ${\displaystyle BD=YF_{1}+YF_{2}=2a,}$ gdzie ${\displaystyle a}$ – duża półoś (korzystamy z równości wynikających z istnienia odpowiednich równoległoboków).

${\displaystyle BD}$ jest średnicą okręgu opisanego na prostokącie ${\displaystyle ABCD,}$ którego środkiem jest ${\displaystyle S}$ więc ${\displaystyle BS=DS=a,}$ co należało pokazać.

Definicja elipsy za pomocą ustalonego punktu, prostej i mimośrodu

Niech będą ustalone na płaszczyźnie: punkt ${\displaystyle F,}$ prosta ${\displaystyle k}$ oraz liczba rzeczywista ${\displaystyle e.}$

Elipsa jest zbiorem punktów płaszczyzny, dla których stosunek odległości od punktu ${\displaystyle F}$ do odległości tych punktów od prostej ${\displaystyle k}$ jest stały i równy ${\displaystyle e,}$ takie że ${\displaystyle 0<e<1;}$ punkt ${\displaystyle F}$ jest wtedy jednym z ognisk elipsy, prosta ${\displaystyle k}$ jej kierownicą, a liczba ${\displaystyle e}$ mimośrodem. Analogicznie dla mimośrodu równego 1 otrzymamy parabolę, dla mimośrodu większego niż 1 otrzymamy hiperbolę.

Uogólnienia

Elipsa jest szczególnym przypadkiem superelipsy. Odpowiednikiem elipsy w przestrzeni trójwymiarowej jest elipsoida.

Zobacz też

Informacje w projektach siostrzanych

Multimedia w Wikimedia Commons

Cytaty w Wikicytatach

Definicje słownikowe w Wikisłowniku

• całka eliptyczna – tu m.in.: Tabela całek eliptycznych zupełnych 2-go rodzaju E(k)
• prawa Keplera
• długość krzywej

Uwagi

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Ellipse, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).
• Grant Sanderson, Why slicing a cone gives an ellipse, 3blue1brown, YouTube, 1 sierpnia 2018 [dostęp 2021-03-14].
• Kalkulator całek eliptycznych online https://keisan.casio.com/exec/system/1180573451