Całki eliptyczne

Całki eliptyczne – ważna klasa całek postaci^[1]:

${\displaystyle \int R\left(x,{\sqrt {W(x)}}\right)dx,}$

(1)

gdzie ${\displaystyle R}$ jest funkcją wymierną zmiennych ${\displaystyle x}$ i ${\displaystyle y={\sqrt {W(x)}},}$ (tj. ${\displaystyle R}$ jest w postaci ilorazu dwóch wielomianów zmiennych ${\displaystyle x}$ i ${\displaystyle y={\sqrt {W(x)}}}$), a ${\displaystyle W(x)}$ jest wielomianem o współczynnikach rzeczywistych stopnia 3 lub 4, tj. ${\displaystyle W(x)=a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0},}$ a ponadto ${\displaystyle W(x)}$ ma pierwiastki jednokrotne.

Całki eliptyczne pojawiają się przy rozwiązywania problemu obliczenia długości łuku elipsy. Stąd wzięły swoją nazwę. W ścisłym znaczeniu nazwa ta dotyczy tylko tych całek postaci (1), których nie dają się wyrazić za pomocą funkcji elementarnych. Całki tej postaci nazywa się pseudoeliptycznymi, jeżeli da się je sprowadzić do funkcji elementarnych. Jest tak, gdy wielomian ${\displaystyle W}$ ma powtarzające się pierwiastki oraz ${\displaystyle R(x,y)}$ nie zawiera nieparzystych potęg ${\displaystyle y.}$

Rodzaje całek eliptycznych

Dowodzi się, że każdą całkę eliptyczną można sprowadzić do sumy całek w postaci elementarnej (która zawiera całki po funkcjach wymiernych) oraz całek nie wyrażających się przez funkcje elementarne, mających trzy możliwe postacie:

• ${\displaystyle \int {\frac {dt}{\sqrt {\left(1-t^{2}\right)\left(1-k^{2}t^{2}\right)}}}\ \ (0<k<1),}$
• ${\displaystyle \int {\frac {\left(1-k^{2}t^{2}\right)dt}{\sqrt {\left(1-t^{2}\right)\left(1-k^{2}t^{2}\right)}}}\ \ (0<k<1),}$
• ${\displaystyle \int {\frac {dt}{\left(1-nt^{2}\right){\sqrt {\left(1-t^{2}\right)\left(1-k^{2}t^{2}\right)}}}}\ \ (0<k<1),\quad {}}$ ${\displaystyle n}$ – dowolna liczba rzeczywista

Liouville dowiódł, że powyższych całek nie da wyrazić się za pomocą funkcji elementarnych.

Legendre zastosował podstawienie ${\displaystyle t=\sin \phi ,}$ dzięki czemu całki te uprościły swoją postać do całek, które nazywamy odpowiednio całką eliptyczną pierwszego, drugiego i trzeciego rodzaju w postaci Legendre’a, tj.

• ${\displaystyle \int {\frac {d\phi }{\sqrt {\left(1-k^{2}\sin ^{2}\phi \right)}}}\ \ (0<k<1)\quad {}}$ – całka eliptyczna 1 rodzaju,
• ${\displaystyle \int {\sqrt {\left(1-k^{2}\sin ^{2}\phi \right)}}\;d\phi \ \ (0<k<1)\quad {}}$ – całka eliptyczna 2 rodzaju,
• ${\displaystyle \int {\frac {d\phi }{\left(1-n\sin ^{2}\phi \right){\sqrt {\left(1-k^{2}\sin ^{2}\phi \right)}}}}\ \ (0<k<1)\quad {}}$ – całka eliptyczna 3 rodzaju.

Szczególnie ważne i często używane są pierwsze dwie.

Całki eliptyczne oznaczone

Całki eliptyczne niezupełne

Powyższe całki eliptyczne 1, 2 i 3 rodzaju traktowane jako całki oznaczone w granicach od 0 do ${\displaystyle \psi }$ oznacza się za Legendre odpowiednio

• ${\displaystyle F(k,\psi )=\int \limits _{0}^{\psi }{\frac {d\phi }{\sqrt {\left(1-k^{2}\sin ^{2}\phi \right)}}}\ \ (0<k<1)\quad {}}$ – całka eliptyczna niezupełna 1 rodzaju,
• ${\displaystyle E(k,\psi )=\int \limits _{0}^{\psi }{\sqrt {\left(1-k^{2}\sin ^{2}\phi \right)}}\;d\phi \ \ (0<k<1)\quad {}}$ – całka eliptyczna niezupełna 2 rodzaju,
• ${\displaystyle \Pi (n;k,\psi )=\int _{0}^{\psi }{\frac {1}{1-n\sin ^{2}\phi }}{\frac {d\phi }{\sqrt {1-k^{2}\sin ^{2}\phi }}}\quad {}}$ – całka eliptyczna niezupełna 3 rodzaju.

Parametr ${\displaystyle k}$ występujący w funkcjach ${\displaystyle F,E,\Pi }$ nazywany jest modułem. Parametr ${\displaystyle n}$ całki ${\displaystyle \Pi (n;k,\psi )}$ nazywany jest charakterystyką – może przyjmować dowolne wartości niezależnie od innych parametrów.

Całki eliptyczne zupełne

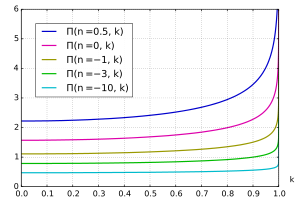
Całki eliptyczne zupełne są szczególnym przypadkiem całek niezupełnych ${\displaystyle F(k,\psi ),E(k,\psi )}$ oraz ${\displaystyle \Pi (n;k,\psi )}$ – oblicza się je podstawiając ${\displaystyle \psi =\pi /2,}$ tj.

• ${\displaystyle K(k)=F\left(k,{\frac {\pi }{2}}\right)=\int \limits _{0}^{\pi /2}{\frac {d\phi }{\sqrt {\left(1-k^{2}\sin ^{2}\phi \right)}}}\ \ (0<k<1)\quad {}}$ – całka eliptyczna zupełna 1 rodzaju,
• ${\displaystyle E(k)=E\left(k,{\frac {\pi }{2}}\right)=\int \limits _{0}^{\pi /2}{\sqrt {\left(1-k^{2}\sin ^{2}\phi \right)}}\;d\phi \ \ (0<k<1)\quad {}}$ – całka eliptyczna zupełna 2 rodzaju,
• ${\displaystyle \Pi (n;k)=\int _{0}^{\frac {\pi }{2}}{\frac {d\phi }{\left(1-n\sin ^{2}\phi \right){\sqrt {1-k^{2}\sin ^{2}\phi }}}}\quad {}}$ – całka eliptyczna zupełna 3 rodzaju

Czasami jednak całki 3 rodzaju definiuje się z odwrotnym znakiem stojącym przed parametrem ${\displaystyle n{:}}$

• ${\displaystyle \Pi (n;k)=\int _{0}^{\frac {\pi }{2}}{\frac {d\phi }{\left(1+n\sin ^{2}\phi \right){\sqrt {1-k^{2}\sin ^{2}\phi }}}}.}$

Wartości całek eliptycznych. Monotoniczność

Wartości całek eliptycznych niezupełnych ${\displaystyle F(k,\psi ),}$ ${\displaystyle E(k,\psi )}$ oraz ${\displaystyle \Pi (n;k,\psi )}$ można obliczyć numerycznie. Dostępne są też kalkulatory online (por. Linki zewnętrzne – na końcu artykułu).

Wartości całek eliptycznych zupełnych ${\displaystyle K(k),}$ ${\displaystyle E(k)}$ oraz ${\displaystyle \Pi (n,k)}$ są stabelaryzowane (por. Tabela całek niżej); można je też znaleźć w niektórych tablicach matematycznych. Dostępne są też kalkulatory online (por. Linki zewnętrzne – na końcu artykułu).

Z wykresów wartości całek przedstawionych tutaj widać, że całka zupełna 1 rodzaju rośnie ze wzrostem ${\displaystyle k;}$ dla ${\displaystyle k=0}$ ma wartość około ${\displaystyle 1{,}6,}$ dla ${\displaystyle k=1}$ rozbiega się do nieskończoności. Całka eliptyczna 2 rodzaju maleje od wartości około ${\displaystyle 1{,}6}$ dla ${\displaystyle k=0}$ do wartości ${\displaystyle 1}$ dla ${\displaystyle k=0.}$ Monotoniczność tych całek wynika wprost z zależności funkcji podcałkowych od parametru ${\displaystyle k{:}}$ dla całki ${\displaystyle K(k)}$ funkcja podcałkowa rośnie ze wzrostem ${\displaystyle k,}$ a dla całki ${\displaystyle E(k)}$ funkcja podcałkowa maleje ze wzrostem ${\displaystyle k.}$

Całka zupełna 3 rodzaju a) dla ${\displaystyle k\neq 1}$ rośnie ze wzrostem ${\displaystyle k}$ dla ${\displaystyle n<1}$ i maleje ze wzrostem ${\displaystyle k}$ dla ${\displaystyle n>1}$ b) dla ${\displaystyle k=1}$ rozbiega się do nieskończoności dla wszystkich wartości ${\displaystyle n.}$

Zastosowania całek eliptycznych

Całka eliptyczna 1 rodzaju

Obliczanie okresu drgań wahadła

Okres drgań wahadła matematycznego zadany jest przez całkę eliptyczną zupełną 1 rodzaju wzorem^[2]:

${\displaystyle T(\theta _{0})=4{\sqrt {\frac {\ell }{g}}}\,\cdot K\left(\sin {\frac {\theta _{0}}{2}}\right),}$

gdzie ${\displaystyle \ell }$ – długość wahadła, ${\displaystyle \theta _{0}}$ – maksymalny kąt odchylenia wahadła od pionu, ${\displaystyle g}$ – przyspieszenie ziemskie.

Z wartości całki ${\displaystyle K(k)}$ wynika (por. Tabela całek niżej), że dla małych amplitud drgań ${\displaystyle K(\sin \theta _{0}/2)\approx K(0)=1{,}5707963=\pi /2,}$ co daje wynik ${\displaystyle T_{0}=2\pi {\sqrt {\ell /g}}}$ – okres drgań nie zależy od amplitudy (izochronizm odkryty przez Galileusza). Jednak ze wzrostem amplitudy okres drgań rośnie. Np. dla ${\displaystyle \theta _{0}=90^{\circ }}$ mamy (por. Tabela całek niżej) ${\displaystyle K(\sin 45^{\circ })\approx K(0{,}707)\approx 1{,}854}$ oraz ${\displaystyle T(90^{\circ })=7{,}416{\sqrt {\ell /g}}=1,18T_{0}.}$ Zaś dla ${\displaystyle \theta _{0}=180^{\circ }}$ (wahadło wznosi się do pionu) mamy ${\displaystyle K(\sin 90^{\circ })=K(1)=+\infty ;}$ stąd ${\displaystyle T=+\infty }$ – wahadło wznosi się od najniższego położenia do pionu nieskończenie długo (tzw. ruch pełzający)^[3].

Całka eliptyczna 2 rodzaju

Obwód elipsy

Obwód elipsy o półosiach ${\displaystyle a,b}$ zadany jest przez całkę eliptyczną zupełną 2 rodzaju wzorem^[4]

${\displaystyle \ell =4a\,E{\big (}e{\big )},}$

gdzie ${\displaystyle e={\sqrt {a^{2}-b^{2}}}/a={\sqrt {1-(b/a)^{2}}}}$ – mimośród elipsy.

Np. dla ${\displaystyle a=2}$ oraz ${\displaystyle b=1}$ mimośród wynosi ${\displaystyle e=0{,}866025.}$ Aby skorzystać z Tabeli całek (por. niżej) obliczamy kąt ${\displaystyle \alpha =\arcsin(k),}$ przy czym ${\displaystyle {\text{k}}\equiv e,}$ co daje ${\displaystyle \alpha =\arcsin(0,866025)\approx 60^{\circ };}$ z tabeli odczytujemy ${\displaystyle E(e)=1{,}2110560,}$ co daje obwód elipsy równy ${\displaystyle l=9{,}688448.}$

Łuk elipsy

(a) Łuk elipsy o półosiach ${\displaystyle a,b,}$ ograniczony kątami ${\displaystyle \alpha _{1},\alpha _{2},}$ mierzonymi od osi ${\displaystyle OX}$ do punktów początkowego i końcowego łuku elipsy, jest zadany przez różnicę całek eliptycznych niezupełnych 2 rodzaju wzorem

${\displaystyle \ell (\alpha _{1},\alpha _{2})=a\,E(e,\psi _{2})-a\,E(e,\psi _{1}),}$

gdzie: ${\displaystyle \psi _{1}=\operatorname {arctg} \left({\frac {a}{b}}\operatorname {tg} (\alpha _{1})\right),}$ ${\displaystyle \psi _{2}=\operatorname {arctg} \left({\frac {a}{b}}\operatorname {tg} (\alpha _{2})\right),}$ ${\displaystyle e={\sqrt {1-(b/a)^{2}}}}$ – mimośród elipsy.

(Wartości parametrów ${\displaystyle \psi _{1},\psi _{2},}$ którym odpowiadają katy ${\displaystyle \phi _{1},\phi _{2}}$ ograniczające łuk elipsy, wynikają z równań parametrycznych elipsy.)

(b) Łuk elipsy o półosiach ${\displaystyle a,b,}$ ograniczony kątami ${\displaystyle \alpha _{1}=0,\alpha _{2},}$ mierzonymi od osi ${\displaystyle OX}$ do punktów początkowego i końcowego łuku elipsy, jest zadany przez całkę eliptyczną niezupełną 2 rodzaju wzorem

${\displaystyle \ell (\alpha _{1}=0,\alpha _{2})=a\,E(e,\psi _{2}),}$

gdzie ${\displaystyle \psi _{2}=\operatorname {arctg} \left({\frac {a}{b}}\operatorname {tg} (\alpha _{2})\right).}$

Całka eliptyczna 3 rodzaju

Długość łuku południka

Długość łuku południka od równika do szerokości geograficznej ${\displaystyle \psi }$ jest określona wzorem:

${\displaystyle d(\psi )=a(1-e^{2})\Pi (e^{2};e^{2},\psi )}$

gdzie ${\displaystyle a}$ jest główną osią elipsy, przechodzącej przez bieguny Ziemi, utworzonej z jej południków; ${\displaystyle e}$ jest mimośrodem tej elipsy.

Całki eliptyczne jako podklasa całek Abela

Całki tego rodzaju, w których za zmienną ${\displaystyle y}$ podstawia się dowolną funkcję algebraiczną zmiennej ${\displaystyle x,}$ taką że

${\displaystyle P(x,y)=0,}$

gdzie ${\displaystyle P(x,y)}$ jest wielomianem względem zmiennych ${\displaystyle x}$ i ${\displaystyle y,}$ nazywa się czasem całkami Abela. Całki eliptyczne są więc podklasą całek Abela.

Funkcje odwrotne do całek eliptycznych

Funkcje odwrotne do różnego typu całek eliptycznych noszą nazwę funkcji eliptycznych. Np. funkcja eliptyczna Weierstrassa ${\displaystyle \wp (z,g_{2},g_{3})}$ zmiennej zespolonej ${\displaystyle z}$ o parametrach ${\displaystyle g_{2},g_{3}}$ jest funkcją odwrotną do funkcji wyrażonej przez całkę

${\displaystyle z(w)=\int \limits _{w}^{\infty }{\frac {dt}{\sqrt {4t^{3}-g_{2}t-g_{3}}}}.}$

W szczególności funkcje odwrotne mają całki eliptyczne niezupełne ${\displaystyle F(k,\psi ),E(k,\psi ),\Pi (n;k,\psi ).}$ Np. funkcjami odwrotnymi do funkcji eliptycznej ${\displaystyle u=F(k,\psi )}$ są funkcje amplitudy ${\displaystyle \psi =am(k,u).}$

Obliczenia numeryczne

Poniżej podano kod programu w C++ liczącego całki eliptyczne zupełne 2-go rodzaju ${\displaystyle E(k)}$ dla ${\displaystyle \alpha =0^{\circ },1^{\circ },\dots ,90^{\circ },}$ gdzie ${\displaystyle k=\sin \alpha .}$ Zastosowano tu prostą metodę całkowania numerycznego – metodę trapezów. Pomimo prostoty uzyskuje się dowolnie duże dokładności, przy odpowiednio dobranej liczbie podziałów przedziału całkowania. Szybciej zbieżne metody numeryczne wykorzystują np. rozwinięcia funkcji podcałkowej w szeregi.

/* Liczenie całek eliptycznych 2 rodzaju E(k) */
#include <iostream>
#include <iomanip>
#include <cmath>

using namespace std;

double f(double t, double k)
{
return sqrt(1-k*k*sin(t)*sin(t));
}

int main()
{
   double t, h, trapez, pole, t1,t2, alfa, alfa_r, k, a, b;
   int m;

   for(int j=0;j<=90;j++)
   {
       alfa=j; //kąt w stopniach
       alfa_r = M_PI/180*alfa;
       k=sin(alfa_r);
       t1=0;        //wartość początkowa przedziału całkowania
       t2=M_PI/2;   //wartość końcowa przedziału całkowania
       m = 10000000;//Liczba podziałów przedziału całkowania
    
       pole = 0;
       h = (t2-t1)/m;
    
       t=t1;
       a=f(t,k);
       
       for(int i=1; i<=m; i++)
       {
           b=f(t+h,k);
           trapez = (a+b)*h/2;
           pole = pole + trapez;
           t=t+h;
           a=b;
       }
       cout << setprecision(7) << fixed;
       cout << " k="<<k<<"  alfa="<<alfa<<"'"<<"  całka E(k)=" << pole << endl;
    }
   return 0;
}

Obliczenia numeryczne całek eliptycznych niezupełnych

(1) W celu obliczenia całki niezupełnej 2-go rodzaju ${\displaystyle E(k,\psi )}$ wystarczy w powyższym kodzie zmienić parametr t2 z wartości M_PI/2 (oznaczającego liczbę π/2) na odpowiednią wartość parametru ${\displaystyle \psi }$ (linia 24 kodu).

(2) W celu obliczenia całki niezupełnej 1-go rodzaju ${\displaystyle F(k,\psi )}$ wystarczy zmienić wartość zwracaną przez funkcję na jej odwrotność (linia 10 kodu) oraz nadać wartość parametru ${\displaystyle \psi }$ (linia 24 kodu).

(3) W celu obliczenia całki niezupełnej 3-go rodzaju ${\displaystyle \Pi (k,n,\psi )}$ wystarczy zmienić wartość zwracaną przez funkcję zgodnie z definicją funkcji podcałkowej tej całki (linia 10 kodu), podstawiając dodatkowo wartość parametru ${\displaystyle n}$ oraz podstawić wartość parametru ${\displaystyle \psi }$ (linia 24 kodu).

Tabela wartości całek eliptycznych

Uwaga: Tutaj ${\displaystyle {\text{k}}=\sin(\alpha )}$

cd. Tabela wartości całek eliptycznych

α°	K(k)	E(k)	α°	K(k)	E(k)	α°	K(k)	E(k)	α°	K(k)	E(k)
51°	1,9538648	1,2962780	61°	2,1842132	1,2015382	71°	2,5507314	1,1096434	81°	3,2553029	1,0337895
52°	1,9728823	1,2869537	62°	2,2131947	1,1920457	72°	2,5998197	1,1010622	82°	3,3698680	1,0278436
53°	1,9926698	1,2775739	63°	2,2435493	1,1825891	73°	2,6521380	1,0926503	83°	3,5004225	1,0223126
54°	2,0132666	1,2681465	64°	2,2753764	1,1731794	74°	2,7080676	1,0844252	84°	3,6518560	1,0172369
55°	2,0347153	1,2586796	65°	2,3087868	1,1638280	75°	2,7680631	1,0764051	85°	3,8317420	1,0126635
56°	2,0570623	1,2491816	66°	2,3439047	1,1545467	76°	2,8326726	1,0686095	86°	4,0527582	1,0086480
57°	2,0803581	1,2396612	67°	2,3808702	1,1453479	77°	2,9025649	1,0610593	87°	4,3386540	1,0052586
58°	2,1046577	1,2301272	68°	2,4198417	1,1362444	78°	2,9785690	1,0537769	88°	4,7427173	1,0025841
59°	2,1300214	1,2205890	69°	2,4609995	1,1272496	79°	3,0617286	1,0467865	89°	5,4349098	1,0007516
60°	2,1565156	1,2110560	70°	2,5045501	1,1183777	80°	3,1533853	1,0401144	90°	${\displaystyle +\infty }$	1,0000000

Zobacz też

• elipsa
• wahadło
• funkcje specjalne

Przypisy

Bibliografia

• I.N. Bronsztejn, K.A. Siemiendiajew, Poradnik encyklopedyczny. Matematyka, PWN, Warszawa 1959, s. 92–93 (Tablice całek), s. 409–410 definicje całek.

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Elliptic Integral, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2024-03-07].