この項目では、複素平面における線積分について説明しています。一般の線積分については「線積分 」をご覧ください。
下記テーマに関する記事の一部 解析学
複素解析 における線積分 (せんせきぶん、英 : line integral )とは、複素平面 内の道に沿った積分 であり[1] [2] [3] ジョルダン曲線 の場合の線積分を周回積分 (しゅうかいせきぶん、英 : contour integral )ということがある。
線積分は複素解析 の手法である留数計算 と密接に関連している[4]
線積分のひとつの使い方として、実変数だけの方法を使うことでは容易には分からない、実数直線に沿った積分の計算がある[5]
線積分の方法は以下を含む。
これらの積分や和を求めるために、これらのうちのひとつ、あるいは、複数を組み合わせた、また、極限をとる様々な方法を使うことができる。
複素平面内の曲線 複素解析 において、積分路 は複素平面 内の曲線の一種である。路に沿う積分では、積分路がその上で積分が適切に定義できる曲線 の正確な定義を与える。複素平面内の曲線 は、実数直線 の閉区間 から複素平面への連続関数 z : [a , b ] → C
曲線のこの定義は、直感的な概念と一致するが、閉区間からの連続関数による径数付けを含む。このより正確な定義により、曲線が積分に有用なためにもたなければならない性質が何であるかを考えることができる。以下の小節では、積分できる曲線を、向きを与えることができる有限個の連続曲線から作ることのできるものだけに絞る。さらに、「断片」は互いに交わらない場合だけを考え、各断片は有限の(消えない)連続微分を持つと仮定する。これらの仮定は次のような曲線だけを考えることと対応する。例えばペンによって、切れ目なく一筆書きで、曲線の新しい断片を始める時だけ止まり、ずっとペンは持ち上げないように、たどることができる[6]
向き付けられた滑らかな曲線 積分路はしばしば向き付けられた滑らかな曲線のことばで定義される[6]
滑らかな曲線 とは、曲線 z : [a , b ] → C z が単射 である)ものである、ただし終点が始点と一致する場合 (z (a ) = z (b )) だけは例外である。終点が始点と一致するような場合には、曲線は閉曲線と呼ばれ、関数は他のいたるところ単射でなければならず、微分はその一致する点で連続でなければならない (z' (a ) = z' (b )) 。閉でない滑らかな曲線はしばしば滑らかな弧と呼ばれる[6]
曲線の径数付け(英語版) により曲線上の点に自然な順序が入る:x < y z (x )z (y )向き付けられた滑らかな曲線 (directed smooth curve) の概念を導く。特定の径数付けに依存しない曲線を考えるのが最も有用である。このことは同じ方向を持つ滑らかな曲線の同値類 を考えることによってなされる。すると方向をもつ滑らかな曲線 は、ある滑らかな曲線の像である複素平面の点の集合に(径数付けから定まる)自然な順序をいれたものとして定義できる。点のすべての順序付けが滑らかな曲線の自然な順序であるわけではないことに注意。実は、与えられた滑らかな曲線は、そのような順序付けを2つしかもたない。また、ひとつの閉曲線は任意の点を終点として持つことができるが、滑らかな弧の終点となるのは2点のみである。
積分路 積分路はその上で路に沿う積分を定義する曲線のクラスである。積分路 は向き付けられた滑らかな曲線の有限列 γ 1 , ..., γ n 1 ≤ i < n に対して γ i γ i +1+ が曲線をつないで新しい曲線を作ることを表すためにしばしば用いられる。したがって n 個の断片からなる積分路 Γ を
Γ = γ 1 + γ 2 + ⋯ + γ n {\displaystyle \Gamma =\gamma _{1}+\gamma _{2}+\cdots +\gamma _{n}} と書くことができる。
路に沿う積分 複素関数 f ː C → C 路に沿う積分 (contour integral , 曲線に沿う積分、線積分)は、実数値関数の積分の一般化である。複素平面 内の連続関数 に対し、路に沿う積分は線積分 の類似で定義することができる。最初に向き付けられた滑らかな曲線に沿った積分を実数値のパラメータの上の積分のことばで定義するのである。より一般的な定義は、区間の分割 との類似による積分路の分割とリーマン積分 のことばにより与えることができる。どちらの場合も路に沿う積分は積分路を構成する向き付けられた滑らかな曲線上の積分の和として定義される。
積分路の終点が始点と一致するとき、路に沿う積分を周回積分ということがある。
連続関数の場合 この方法で路に沿う積分を定義するためにはまず実変数上の複素数値関数の積分を考えなければならない。f : R → C t の複素数値関数とする。f の実部と虚部はしばしばそれぞれ u (t )v (t )
f ( t ) = u ( t ) + i v ( t ) {\displaystyle f(t)=u(t)+iv(t)} である。すると複素数値関数 f の区間 [a , b ] 上の積分は次で与えられる:
∫ a b f ( t ) d t = ∫ a b [ u ( t ) + i v ( t ) ] d t = ∫ a b u ( t ) d t + i ∫ a b v ( t ) d t . {\displaystyle {\begin{aligned}\int _{a}^{b}f(t)\,dt&=\int _{a}^{b}{\big [}u(t)+iv(t){\big ]}\,dt\\&=\int _{a}^{b}u(t)\,dt+i\int _{a}^{b}v(t)\,dt.\end{aligned}}} f : C → C 向き付けられた滑らかな曲線 γ 上の連続関数 とする。z : R → C γ の任意の径数付けとする。すると γ に沿った積分は
∫ γ f ( z ) d z {\displaystyle \int _{\gamma }f(z)\,dz\,} と記され、
∫ γ f ( z ) d z = ∫ a b f ( z ( t ) ) z ′ ( t ) d t {\displaystyle \int _{\gamma }f(z)\,dz=\int _{a}^{b}f(z(t))z'(t)\,dt} によって与えられる[6]
この定義は well defined である。つまり、結果は選ばれた径数付けに依存しない[6] γ に沿う積分は存在しないと言われる。
リーマン積分の一般化として リーマン積分 の複素変数の関数への一般化は実数からの関数に対する定義との完全な類似でなされる。向き付けられた滑らかな曲線 γ の分割は γ 上の有限個の順序付けられた点の集合と定義される。その曲線上の積分は分割の点での関数値の有限和の極限である。極限は分割の連続する2点の(複素平面での)距離(分割の幅)の最大値が 0 に行くようにとる。
直接的な方法 直接的な方法は多変数解析学における線積分の計算と類似の手法による積分計算を含む。これは以下の手法を用いることを意味する:
積分路は実変数の微分可能な複素数値関数によって径数付けられる、あるいは積分路は断片に分けられ別々に径数付けられる。 径数付けを被積分関数に代入することで積分が一実変数の積分となる。 積分は実変数の積分と類似の手法で計算される。 例 複素解析における基本的な結果は z −1 2πi であることである、ただし積分路は単位円周を反時計回りに一周するものをとる(あるいは 0 についての任意の正の向きのジョルダン曲線 でもよい)。単位円周の場合には積分
∮ C 1 z d z {\displaystyle \oint _{C}{1 \over z}\,dz} を計算する直接的な方法がある。この積分の計算では、単位円周 |z | = 1 を z (t ) = eit (t ∈ [0, 2π ])dz /dt = ieit
∮ C 1 z d z = ∫ 0 2 π 1 e i t i e i t d t = i ∫ 0 2 π d t = 2 π i . {\displaystyle \oint _{C}{1 \over z}\,dz=\int _{0}^{2\pi }{\frac {1}{e^{it}}}ie^{it}\,dt=i\int _{0}^{2\pi }dt=2\pi i.} 積分定理の応用 路に沿う積分を計算するために積分定理を用いることもしばしばある。これは実数値関数が路に沿う積分の計算と一緒に同時に計算されることを意味する。
コーシーの積分公式 や留数定理 のような積分定理は以下の手法において一般的に用いられる:
積分路は以下のように選ばれる。実数値積分を記述する複素平面の部分を通り、コーシーの積分公式 や留数定理 が使えるように被積分関数の特異点を囲む。 積分は各極のまわりの小さい円周に沿う積分のみに簡約される。 これらの積分公式を適用することで積分路全体の積分の値が得られる。 積分路の全体は前に選んだように実数値積分を記述する複素平面の部分を通る積分路 R と複素平面をお横断する積分路 I に分割できる。積分路全体上の積分はこれらの積分路それぞれの上の積分の和である。 I 上の積分が 0 であることを示すことができるか、あるいは、求める実数値積分が広義積分のときは I 上の積分が 0 に収束することを示せば、R 上の積分は積分路 R + I 上記の段階を示すことができれば、R 上の実数値積分を計算することができる。 例 次の積分を考える:
∫ − ∞ ∞ 1 ( x 2 + 1 ) 2 d x . {\displaystyle \int _{-\infty }^{\infty }{1 \over (x^{2}+1)^{2}}dx.} この積分を計算するために、次の複素数値関数を見る:
f ( z ) = 1 ( z 2 + 1 ) 2 . {\displaystyle f(z)={1 \over (z^{2}+1)^{2}}.} この関数は i −i に特異点を持つ。積分路として実数値積分を含む積分路を選ぶ。ここでは実数直線上に境界の直径(−a から a まで)を持つ半円が便利である。この積分路を C と呼ぶ。
2つのやり方がある。コーシーの積分公式 を使う方法と留数の手法によるものである:
コーシーの積分公式を使う 次に注意:
∮ C f ( z ) d z = ∫ − a a f ( z ) d z + ∫ Arc f ( z ) d z {\displaystyle \oint _{C}f(z)\,dz=\int _{-a}^{a}f(z)\,dz+\int _{\text{Arc}}f(z)\,dz} したがって
∫ − a a f ( z ) d z = ∮ C f ( z ) d z − ∫ Arc f ( z ) d z . {\displaystyle \int _{-a}^{a}f(z)\,dz=\oint _{C}f(z)\,dz-\int _{\text{Arc}}f(z)\,dz.} さらに次が成り立つ:
f ( z ) = 1 ( z 2 + 1 ) 2 = 1 ( z + i ) 2 ( z − i ) 2 . {\displaystyle f(z)={1 \over (z^{2}+1)^{2}}={1 \over (z+i)^{2}(z-i)^{2}}.} 閉曲線の囲む領域内に二位の極 i があるため、コーシーの積分公式を用いて、
∮ C f ( z ) d z = 2 π i d d z ( 1 ( z + i ) 2 ) | z = i = 2 π i ( − 2 ( z + i ) 3 ) | z = i = π 2 . {\displaystyle \oint _{C}f(z)\,dz=2\pi i{\frac {d}{dz}}\left({1 \over (z+i)^{2}}\right){\Bigg |}_{z=i}=2\pi i\left({\frac {-2}{(z+i)^{3}}}\right){\Bigg |}_{z=i}={\frac {\pi }{2}}.} 半円の弧を Arc と呼ぶことにすれば、Arc 上の積分が R → ∞0 に収束することを示す必要がある。estimation lemma(英語版) を用いて
| ∫ Arc f ( z ) d z | ≤ M L {\displaystyle \left|\int _{\text{Arc}}f(z)\,dz\right|\leq ML} ただし M は Arc 上の |f (z )| の上界であり、L は Arc の長さである。今
| ∫ Arc f ( z ) d z | ≤ R π ( R 2 − 1 ) 2 → 0 ( R → ∞ ) {\displaystyle \left|\int _{\text{Arc}}f(z)\,dz\right|\leq {\frac {R\pi }{(R^{2}-1)^{2}}}\to 0\quad (R\to \infty )} である。したがって
∫ − ∞ ∞ 1 ( x 2 + 1 ) 2 d x = ∫ − ∞ ∞ f ( z ) d z = lim a → + ∞ ∫ − a a f ( z ) d z = π 2 . ◻ {\displaystyle \int _{-\infty }^{\infty }{1 \over (x^{2}+1)^{2}}\,dx=\int _{-\infty }^{\infty }f(z)\,dz=\lim _{a\to +\infty }\int _{-a}^{a}f(z)\,dz={\pi \over 2}.\quad \square } 留数の方法を使う i の周りでの f (z )ローラン展開 を考える(i は考える必要のある唯一の特異点である)。すると
f ( z ) = − 1 4 ( z − i ) 2 + − i 4 ( z − i ) + 3 16 + i 8 ( z − i ) + − 5 64 ( z − i ) 2 + ⋯ {\displaystyle f(z)={-1 \over 4(z-i)^{2}}+{-i \over 4(z-i)}+{3 \over 16}+{i \over 8}(z-i)+{-5 \over 64}(z-i)^{2}+\cdots } となる(この級数の導出はローラン級数 (英語版)
留数が −i /4 であることは見た目から明らかである(これを確かめるには、上の等式に z − i 0 でない値となる)。よって留数定理 より
∮ C f ( z ) d z = ∮ C 1 ( z 2 + 1 ) 2 d z = 2 π i R e s z = i f = π 2 . ◻ {\displaystyle \oint _{C}f(z)\,dz=\oint _{C}{1 \over (z^{2}+1)^{2}}\,dz=2\pi i\,\mathrm {Res} _{z=i}f={\frac {\pi }{2}}.\quad \square } したがって前と同じ結果が得られた。
積分路についての注意 余談ではあるが、他の 特異点 −i を囲む半円を取らなかったことについて疑問が生じ得る。正しい向きに動いて実軸に沿って積分するには、その積分路は時計回り、つまり負の方向にまわらなければならず、積分全体の符号が逆になる。
これは級数による留数の手法の使用に影響しない。
例 II: コーシー分布 積分
∫ − ∞ ∞ e i t x x 2 + 1 d x {\displaystyle \int _{-\infty }^{\infty }{e^{itx} \over x^{2}+1}\,dx} 積分路 (確率論 においてコーシー分布 の特性関数のスカラー倍として生じる)は初等解析学 のテクニックでは困難である。それを次の積分路 C に沿った線積分の極限として表示することにより計算しよう:実数直線を −a から a まで沿って行き、0 を中心とする半円に沿って a から −a まで反時計回りに行く。a を 1 よりも大きく取って、虚数単位 i が曲線の内側に入るようにする。線積分は
∫ C e i t z z 2 + 1 d z {\displaystyle \int _{C}{e^{itz} \over z^{2}+1}\,dz} である。eitz は整関数 (複素平面のどこにも特異点を持たない)だから、この関数は分母 z 2 + 10 になる点でのみ特異点を持つ。z 2 + 1 = (z + i )(z − i )z = i z = −i f (z )z = i 留数 は
R e s z = i f ( z ) = lim z → i ( z − i ) f ( z ) = lim z → i e i t z z + i = e − t 2 i {\displaystyle \mathrm {Res} _{z=i}f(z)=\lim _{z\to i}(z-i)f(z)=\lim _{z\to i}{e^{itz} \over z+i}={e^{-t} \over 2i}} である。留数定理 により、
∫ C f ( z ) d z = 2 π i Res z = i f ( z ) = π e − t {\displaystyle \int _{C}f(z)\,dz=2\pi i\operatorname {Res} _{z=i}f(z)=\pi e^{-t}} となる。積分路 C は「まっすぐな (straight)」部分と曲がった弧 (arc) とに分けられるので
∫ straight + ∫ arc = π e − t {\displaystyle \int _{\text{straight}}+\int _{\text{arc}}=\pi e^{-t}} でありしたがって
∫ − a a = π e − t − ∫ arc {\displaystyle \int _{-a}^{a}=\pi e^{-t}-\int _{\text{arc}}} となる。t > 0
∫ arc e i t z z 2 + 1 d z → 0 as a → ∞ {\displaystyle \int _{\text{arc}}{e^{itz} \over z^{2}+1}\,dz\rightarrow 0{\text{ as }}a\rightarrow \infty } であることを示すことができる。よって t > 0
∫ − ∞ ∞ e i t x x 2 + 1 d x = π e − t {\displaystyle \int _{-\infty }^{\infty }{e^{itx} \over x^{2}+1}\,dx=\pi e^{-t}} である。t < 0i ではなく −i をまわる弧を用いた類似の議論によって
∫ − ∞ ∞ e i t x x 2 + 1 d x = π e t {\displaystyle \int _{-\infty }^{\infty }{e^{itx} \over x^{2}+1}\,dx=\pi e^{t}} が示される。よって最終的に次を得る:
∫ − ∞ ∞ e i t x x 2 + 1 d x = π e − | t | . ◻ {\displaystyle \int _{-\infty }^{\infty }{e^{itx} \over x^{2}+1}\,dx=\pi e^{-\left|t\right|}.\quad \square } (t = 0π である。)
例 III: 三角関数の積分 三角関数 を含む積分に対して、ある種の代入を行って複素有理関数へと変換することで積分値が算出できる場合がある。
例として次のような積分を考える。
∫ − π π 1 1 + 3 ( cos t ) 2 d t . {\displaystyle \int _{-\pi }^{\pi }{1 \over 1+3(\cos {t})^{2}}\,dt.} z = eit と変数変換する。
cos t = 1 2 ( e i t + e − i t ) = 1 2 ( z + 1 z ) {\displaystyle \cos t={1 \over 2}\left(e^{it}+e^{-it}\right)={1 \over 2}\left(z+{1 \over z}\right)} および
d z d t = i z , d t = d z i z {\displaystyle {dz \over dt}=iz,\ dt={dz \over iz}} であることを思い出すと、代入により積分は次のように書き直せる。C は単位円周。
∮ C 1 1 + 3 ( 1 2 ( z + 1 z ) ) 2 d z i z = ∮ C 1 1 + 3 4 ( z + 1 z ) 2 1 i z d z = ∮ C − i z + 3 4 z ( z + 1 z ) 2 d z = − i ∮ C 1 z + 3 4 z ( z 2 + 2 + 1 z 2 ) d z = − i ∮ C 1 z + 3 4 ( z 3 + 2 z + 1 z ) d z = − i ∮ C 1 3 4 z 3 + 5 2 z + 3 4 z d z = − i ∮ C 4 3 z 3 + 10 z + 3 z d z = − 4 i ∮ C 1 3 z 3 + 10 z + 3 z d z = − 4 i ∮ C z 3 z 4 + 10 z 2 + 3 d z = − 4 i ∮ C z 3 ( z + 3 i ) ( z − 3 i ) ( z + i 3 ) ( z − i 3 ) d z = − 4 3 i ∮ C z ( z + 3 i ) ( z − 3 i ) ( z + i 3 ) ( z − i 3 ) d z . {\displaystyle {\begin{aligned}\oint _{C}{1 \over 1+3({1 \over 2}(z+{1 \over z}))^{2}}\,{dz \over iz}&=\oint _{C}{1 \over 1+{3 \over 4}(z+{1 \over z})^{2}}{1 \over iz}\,dz\\&=\oint _{C}{-i \over z+{3 \over 4}z(z+{1 \over z})^{2}}\,dz\\&=-i\oint _{C}{1 \over z+{3 \over 4}z(z^{2}+2+{1 \over z^{2}})}\,dz\\&=-i\oint _{C}{1 \over z+{3 \over 4}(z^{3}+2z+{1 \over z})}\,dz\\&=-i\oint _{C}{1 \over {3 \over 4}z^{3}+{5 \over 2}z+{3 \over 4z}}\,dz\\&=-i\oint _{C}{4 \over 3z^{3}+10z+{3 \over z}}\,dz\\&=-4i\oint _{C}{1 \over 3z^{3}+10z+{3 \over z}}\,dz\\&=-4i\oint _{C}{z \over 3z^{4}+10z^{2}+3}\,dz\\&=-4i\oint _{C}{z \over 3(z+{\sqrt {3}}i)\left(z-{\sqrt {3}}i\right)\left(z+{\frac {i}{\sqrt {3}}}\right)\left(z-{\frac {i}{\sqrt {3}}}\right)}\,dz\\&=-{4 \over 3}i\oint _{C}{z \over (z+{\sqrt {3}}i)(z-{\sqrt {3}}i)\left(z+{\frac {i}{\sqrt {3}}}\right)\left(z-{\frac {i}{\sqrt {3}}}\right)}\,dz.\end{aligned}}} 考える必要がある特異点は 3−1/2 i , −3−1/2 i の2つである。
C 1 を 3−1/2 i を囲む小さな円周、C 2 を −3−1/2 i を囲む小さな円周として、以下のように計算できる。
− 4 3 i [ ∮ C 1 z ( z + 3 i ) ( z − 3 i ) ( z + i 3 ) z − i 3 d z + ∮ C 2 z ( z + 3 i ) ( z − 3 i ) ( z − i 3 ) z + i 3 d z ] = − 4 3 i [ 2 π i ( z ( z + 3 i ) ( z − 3 i ) ( z + i 3 ) ) | z = i 3 + 2 π i ( z ( z + 3 i ) ( z − 3 i ) ( z − i 3 ) ) | z = − i 3 ] = 8 π 3 [ i 3 ( i 3 + 3 i ) ( i 3 − 3 i ) ( i 3 + i 3 ) + − i 3 ( − i 3 + 3 i ) ( − i 3 − 3 i ) ( − i 3 − i 3 ) ] = 8 π 3 [ i 3 ( 4 3 i ) ( − 2 i 3 ) ( 2 3 i ) + − i 3 ( 2 3 i ) ( − 4 3 i ) ( − 2 3 i ) ] = 8 π 3 [ i 3 i ( 4 3 ) ( 2 3 ) ( 2 3 ) + − i 3 − i ( 2 3 ) ( 4 3 ) ( 2 3 ) ] = 8 π 3 [ 1 3 ( 4 3 ) ( 2 3 ) ( 2 3 ) + 1 3 ( 2 3 ) ( 4 3 ) ( 2 3 ) ] = 8 π 3 [ 1 3 16 3 3 + 1 3 16 3 3 ] = 8 π 3 [ 3 16 + 3 16 ] = π . {\displaystyle {\begin{aligned}&-{\frac {4}{3}}i\left[\oint _{C_{1}}{\frac {\frac {z}{(z+{\sqrt {3}}i)(z-{\sqrt {3}}i)\left(z+{\frac {i}{\sqrt {3}}}\right)}}{z-{\frac {i}{\sqrt {3}}}}}\,dz+\oint _{C_{2}}{\frac {\frac {z}{(z+{\sqrt {3}}i)(z-{\sqrt {3}}i)\left(z-{\frac {i}{\sqrt {3}}}\right)}}{z+{\frac {i}{\sqrt {3}}}}}\,dz\right]\\&=-{\frac {4}{3}}i\left[2\pi i\left({\frac {z}{(z+{\sqrt {3}}i)(z-{\sqrt {3}}i)(z+{\frac {i}{\sqrt {3}}})}}\right){\Bigg |}_{z={\frac {i}{\sqrt {3}}}}+2\pi i\left({\frac {z}{(z+{\sqrt {3}}i)(z-{\sqrt {3}}i)(z-{\frac {i}{\sqrt {3}}})}}\right){\Bigg |}_{z=-{\frac {i}{\sqrt {3}}}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{({\frac {i}{\sqrt {3}}}+{\sqrt {3}}i)({\frac {i}{\sqrt {3}}}-{\sqrt {3}}i)({\frac {i}{\sqrt {3}}}+{\frac {i}{\sqrt {3}}})}}+{\frac {-{\frac {i}{\sqrt {3}}}}{(-{\frac {i}{\sqrt {3}}}+{\sqrt {3}}i)(-{\frac {i}{\sqrt {3}}}-{\sqrt {3}}i)(-{\frac {i}{\sqrt {3}}}-{\frac {i}{\sqrt {3}}})}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{({\frac {4}{\sqrt {3}}}i)(-{\frac {2}{i{\sqrt {3}}}})({\frac {2}{{\sqrt {3}}i}})}}+{\frac {-{\frac {i}{\sqrt {3}}}}{({\frac {2}{\sqrt {3}}}i)(-{\frac {4}{\sqrt {3}}}i)(-{\frac {2}{\sqrt {3}}}i)}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{i({\frac {4}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})}}+{\frac {-{\frac {i}{\sqrt {3}}}}{-i({\frac {2}{\sqrt {3}}})({\frac {4}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {1}{\sqrt {3}}}{({\frac {4}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})}}+{\frac {\frac {1}{\sqrt {3}}}{({\frac {2}{\sqrt {3}}})({\frac {4}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {1}{\sqrt {3}}}{\frac {16}{3{\sqrt {3}}}}}+{\frac {\frac {1}{\sqrt {3}}}{\frac {16}{3{\sqrt {3}}}}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {3}{16}}+{\frac {3}{16}}\right]=\pi .\end{aligned}}} 例 IIIa: 三角関数の積分、一般的な手続き 上記の方法は、次の形をした全ての積分に適用できる。
∫ 0 2 π P ( sin ( t ) , sin ( 2 t ) , … , cos ( t ) , cos ( 2 t ) , … ) Q ( sin ( t ) , sin ( 2 t ) , … , cos ( t ) , cos ( 2 t ) , … ) d t {\displaystyle \int _{0}^{2\pi }{\frac {P(\sin(t),\sin(2t),\ldots ,\cos(t),\cos(2t),\ldots )}{Q(\sin(t),\sin(2t),\ldots ,\cos(t),\cos(2t),\ldots )}}\,dt} ここで P と Q は多項式である(つまり、三角関数の有理関数の積分を考えている)。積分範囲は先の例のように π から -π まででも良いし、また 2π だけ離れた任意の区間でも良い。
変数変換 z = exp ( i t ) {\displaystyle z=\exp(it)} d z = i exp ( i t ) d t {\displaystyle dz=i\exp(it)\,dt}
1 i z d z = d t . {\displaystyle {\frac {1}{iz}}\,dz=dt.} この変換により閉区間 [0, 2π] は複素平面の単位円周に写される。さらに、
sin ( k t ) = exp ( i k t ) − exp ( − i k t ) 2 i = z k − z − k 2 i {\displaystyle \sin(kt)={\frac {\exp(ikt)-\exp(-ikt)}{2i}}={\frac {z^{k}-z^{-k}}{2i}}} および
cos ( k t ) = exp ( i k t ) + exp ( − i k t ) 2 = z k + z − k 2 {\displaystyle \cos(kt)={\frac {\exp(ikt)+\exp(-ikt)}{2}}={\frac {z^{k}+z^{-k}}{2}}} であるから、変換によって z の有理関数 f (z ) が得られ、積分は
∮ | z | = 1 f ( z ) 1 i z d z {\displaystyle \oint _{|z|=1}f(z){\frac {1}{iz}}\,dz} となる。この積分は f ( z ) 1 i z {\displaystyle f(z){\frac {1}{iz}}}
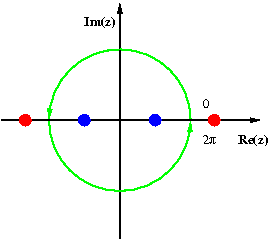
右の図は
I = ∫ 0 π 2 1 1 + sin ( t ) 2 d t , {\displaystyle I=\int _{0}^{\frac {\pi }{2}}{\frac {1}{1+\sin(t)^{2}}}\,dt,} の場合を図示したものである。まず、
I = 1 4 ∫ 0 2 π 1 1 + sin ( t ) 2 d t . {\displaystyle I={\frac {1}{4}}\int _{0}^{2\pi }{\frac {1}{1+\sin(t)^{2}}}\,dt.} と変形して、変数変換をすると
1 4 ∮ | z | = 1 4 i z z 4 − 6 z 2 + 1 d z = ∮ | z | = 1 i z z 4 − 6 z 2 + 1 d z {\displaystyle {\frac {1}{4}}\oint _{|z|=1}{\frac {4iz}{z^{4}-6z^{2}+1}}\,dz=\oint _{|z|=1}{\frac {iz}{z^{4}-6z^{2}+1}}\,dz} となる。被積分関数の極は 1 ± √2 と −1 ± √2 である。これらのうち 1 + √2 と −1 −√2 は単位円板の外側にあり(赤い点で示した。縮尺は正確ではない)、一方 1 − √2 と −1 + √2 は単位円板の内側にある(青い点で示した)。
対応する留数はいずれも −i √2/16 だから、求める積分値は
I = 2 π i 2 ( − 2 16 i ) = π 2 4 {\displaystyle I=2\pi i\;2\left(-{\frac {\sqrt {2}}{16}}i\right)=\pi {\frac {\sqrt {2}}{4}}} となる。
例 IV: 分岐切断 実関数積分
∫ 0 ∞ x x 2 + 6 x + 8 d x . {\displaystyle \int _{0}^{\infty }{{\sqrt {x}} \over x^{2}+6x+8}\,dx.} を考える。次のように複素積分として書き直すところから始める。
∫ C z z 2 + 6 z + 8 d z = I . {\displaystyle \int _{C}{{\sqrt {z}} \over z^{2}+6z+8}\,dz=I.} 問題となる留数の値を得るため、再びコーシーの積分公式もしくは留数定理を用いることができる。しかしここで注意すべき重要なことは、z 1/2 = e (1/2)Log(z ) であり、z 1/2 には分岐切断があるということである。このことは、積分路 C の選び方に影響してくる。
対数関数の分岐切断は、普通は実軸のうち負の部分と定めることが多いが、こうすると計算がやや面倒になる。そこでここでは、実軸の正の部分と定めることにする。
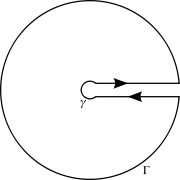
ここで、次のような経路を順にたどって得られる、いわゆる「鍵穴積分路(keyhole contour)」を用いる。
原点を中心として時計回りにほぼ1周する半径 ε の小さな円 実軸に上半平面側から接近して(接触はしていない)平行な線分 反時計回りにほぼ1周する半径 R の大きな円 実軸に下半平面側から接近し平行な線分 z = −2 と z = −4 は大円が囲む内部にあることに注意する。被積分関数の分母を因数分解すれば、これらが2個の極だとがわかる。分岐点は z = 0 だが、これは原点を迂回したことによって避けられている。
γ を半径 ε の小円、Γ を半径 R の大円とする。このとき積分路は
∫ C = ∫ ε R + ∫ Γ + ∫ R ε + ∫ γ {\displaystyle \int _{C}=\int _{\varepsilon }^{R}+\int _{\Gamma }+\int _{R}^{\varepsilon }+\int _{\gamma }} と分解できる。
Γ と γ に沿う積分は、先に行ったのと同様の議論で ε → 0, R → ∞ のときにいずれも 0 に収束することが示せて、積分は2項のみが残る。ここで z 1/2 = e (1/2)Log(z ) であり、分岐切断の外側で γ に沿って動くとき、偏角は 2π だけ変わる。よって
∫ R ε z z 2 + 6 z + 8 d z = ∫ R ε e 1 2 L o g ( z ) z 2 + 6 z + 8 d z = ∫ R ε e 1 2 ( log | z | + i arg z ) z 2 + 6 z + 8 d z = ∫ R ε e 1 2 log | z | e ( 1 / 2 ) ( 2 π i ) z 2 + 6 z + 8 d z = ∫ R ε e 1 2 log | z | e π i z 2 + 6 z + 8 d z = ∫ R ε − z z 2 + 6 z + 8 d z = ∫ ε R z z 2 + 6 z + 8 d z . {\displaystyle {\begin{aligned}\int _{R}^{\varepsilon }{{\sqrt {z}} \over z^{2}+6z+8}\,dz&=\int _{R}^{\varepsilon }{e^{{1 \over 2}\mathrm {Log} (z)} \over z^{2}+6z+8}\,dz\\&=\int _{R}^{\varepsilon }{e^{{1 \over 2}(\log {|z|}+i\arg {z})} \over z^{2}+6z+8}\,dz\\&=\int _{R}^{\varepsilon }{e^{{1 \over 2}\log {|z|}}e^{(1/2)(2\pi i)} \over z^{2}+6z+8}\,dz\\&=\int _{R}^{\varepsilon }{e^{{1 \over 2}\log {|z|}}e^{\pi i} \over z^{2}+6z+8}\,dz\\&=\int _{R}^{\varepsilon }{-{\sqrt {z}} \over z^{2}+6z+8}\,dz\\&=\int _{\varepsilon }^{R}{{\sqrt {z}} \over z^{2}+6z+8}\,dz.\end{aligned}}} ゆえに[注釈 1]
∫ C z z 2 + 6 z + 8 d z = 2 ∫ 0 ∞ x x 2 + 6 x + 8 d x {\displaystyle \int _{C}{{\sqrt {z}} \over z^{2}+6z+8}\,dz=2\int _{0}^{\infty }{{\sqrt {x}} \over x^{2}+6x+8}\,dx} 留数定理を使うか、もしくはコーシーの積分公式を使う(まず被積分関数を部分分数分解して、2個の単純な円の周りの積分に書き直してから和をとる)かして、
π i ( i 2 − i ) = ∫ 0 ∞ x x 2 + 6 x + 8 d x = π ( 1 − 1 2 ) . ◻ {\displaystyle \pi i\left({i \over {\sqrt {2}}}-i\right)=\int _{0}^{\infty }{{\sqrt {x}} \over x^{2}+6x+8}\,dx=\pi \left(1-{1 \over {\sqrt {2}}}\right).\quad \square } を得る。
例 V: 対数関数の平方を利用した積分 この節では、
∫ 0 ∞ log ( x ) ( 1 + x 2 ) 2 d x {\displaystyle \int _{0}^{\infty }{\frac {\log(x)}{(1+x^{2})^{2}}}\,dx} のようなタイプの積分を扱う。
この積分を計算するのに、関数
f ( z ) = ( log ( z ) 1 + z 2 ) 2 {\displaystyle f(z)=\left({\frac {\log(z)}{1+z^{2}}}\right)^{2}} を用い、 − π < arg ( z ) ≤ π {\displaystyle -\pi <\arg(z)\leq \pi }
f (z ) の、右の図に示すような鍵穴積分路に沿った複素線積分を計算する。この積分は、冒頭に示した実積分の定数倍であることがわかり(後述)、積分値は留数定理により
( ∫ R + ∫ M + ∫ N + ∫ r ) f ( z ) d z = 2 π i ( R e s z = i f ( z ) + R e s z = − i f ( z ) ) = 2 π i ( − π 4 + 1 16 i π 2 − π 4 − 1 16 i π 2 ) = − i π 2 {\displaystyle {\begin{aligned}\left(\int _{R}+\int _{M}+\int _{N}+\int _{r}\right)f(z)\,dz&=2\pi i\left(\mathrm {Res} _{z=i}f(z)+\mathrm {Res} _{z=-i}f(z)\right)\\&=2\pi i\left(-{\frac {\pi }{4}}+{\frac {1}{16}}i\pi ^{2}-{\frac {\pi }{4}}-{\frac {1}{16}}i\pi ^{2}\right)\\&=-i\pi ^{2}\end{aligned}}} と計算できる。
R と r をそれぞれ大円、小円の半径とし、上側の線分を M 、下側の線分を N と書く。R → ∞ および r → 0 の極限はまだとっていない。2つの円周部分からの積分の寄与はいずれも極限をとると消える。例えば、ML補題により大円に沿った積分は次のように上から抑えられる:
| ∫ R f ( z ) d z | ≤ 2 π R ( log ( R ) ) 2 + π 2 ( R 2 − 1 ) 2 → 0 {\displaystyle \left|\int _{R}f(z)\,dz\right|\leq 2\pi R{\frac {(\log(R))^{2}+\pi ^{2}}{(R^{2}-1)^{2}}}\to 0} M , N に沿った積分値を計算するため、M 上では z = − x + i ϵ {\displaystyle z=-x+i\epsilon } N 上では z = − x − i ϵ {\displaystyle z=-x-i\epsilon } x < ∞) ととると、
− i π 2 = ( ∫ R + ∫ M + ∫ N + ∫ r ) f ( z ) d z = ( ∫ M + ∫ N ) f ( z ) d z ∫ R , ∫ r vanish = − ∫ ∞ 0 ( log ( − x + i ϵ ) 1 + ( − x + i ϵ ) 2 ) 2 d x − ∫ 0 ∞ ( log ( − x − i ϵ ) 1 + ( − x − i ϵ ) 2 ) 2 d x = ∫ 0 ∞ ( log ( − x + i ϵ ) 1 + ( − x + i ϵ ) 2 ) 2 d x − ∫ 0 ∞ ( log ( − x − i ϵ ) 1 + ( − x − i ϵ ) 2 ) 2 d x = ∫ 0 ∞ ( log ( x ) + i π 1 + x 2 ) 2 d x − ∫ 0 ∞ ( log ( x ) − i π 1 + x 2 ) 2 d x ϵ → 0 = ∫ 0 ∞ ( log ( x ) + i π ) 2 − ( log ( x ) − i π ) 2 ( 1 + x 2 ) 2 d x = ∫ 0 ∞ 4 π i log ( x ) ( 1 + x 2 ) 2 d x = 4 π i ∫ 0 ∞ log ( x ) ( 1 + x 2 ) 2 d x {\displaystyle {\begin{aligned}-i\pi ^{2}&=\left(\int _{R}+\int _{M}+\int _{N}+\int _{r}\right)f(z)\,dz\\&=\left(\int _{M}+\int _{N}\right)f(z)\,dz\qquad \int _{R},\int _{r}{\text{ vanish}}\\&=-\int _{\infty }^{0}\left({\frac {\log(-x+i\epsilon )}{1+(-x+i\epsilon )^{2}}}\right)^{2}\,dx-\int _{0}^{\infty }\left({\frac {\log(-x-i\epsilon )}{1+(-x-i\epsilon )^{2}}}\right)^{2}\,dx\\&=\int _{0}^{\infty }\left({\frac {\log(-x+i\epsilon )}{1+(-x+i\epsilon )^{2}}}\right)^{2}\,dx-\int _{0}^{\infty }\left({\frac {\log(-x-i\epsilon )}{1+(-x-i\epsilon )^{2}}}\right)^{2}\,dx\\&=\int _{0}^{\infty }\left({\frac {\log(x)+i\pi }{1+x^{2}}}\right)^{2}\,dx-\int _{0}^{\infty }\left({\frac {\log(x)-i\pi }{1+x^{2}}}\right)^{2}\,dx\qquad \epsilon \to 0\\&=\int _{0}^{\infty }{\frac {(\log(x)+i\pi )^{2}-(\log(x)-i\pi )^{2}}{(1+x^{2})^{2}}}\,dx\\&=\int _{0}^{\infty }{\frac {4\pi i\log(x)}{(1+x^{2})^{2}}}\,dx\\&=4\pi i\int _{0}^{\infty }{\frac {\log(x)}{(1+x^{2})^{2}}}\,dx\end{aligned}}} 以上より
∫ 0 ∞ log ( x ) ( 1 + x 2 ) 2 d x = − π 4 . {\displaystyle \int _{0}^{\infty }{\frac {\log(x)}{(1+x^{2})^{2}}}\,dx=-{\frac {\pi }{4}}.} 例 VI: 対数関数と、無限遠点での留数 次の積分を計算したい。
I = ∫ 0 3 x 3 4 ( 3 − x ) 1 4 5 − x d x . {\displaystyle I=\int _{0}^{3}{\frac {x^{\frac {3}{4}}(3-x)^{\frac {1}{4}}}{5-x}}\,dx.} これには、関数
f ( z ) = z 3 4 ( 3 − z ) 1 4 . {\displaystyle f(z)=z^{\frac {3}{4}}(3-z)^{\frac {1}{4}}.} の精密な分析が必要である。f (z ) を、分岐切断が図に赤で示したように [0, 3] となるよう構成する。これをするため、2つの対数関数を、枝がそれぞれ
z 3 4 = exp ( 3 4 log ( z ) ) where − π ≤ arg ( z ) < π {\displaystyle z^{\frac {3}{4}}=\exp \left({\frac {3}{4}}\log(z)\right)\quad {\mbox{where}}\quad -\pi \leq \arg(z)<\pi } ( 3 − z ) 1 4 = exp ( 1 4 log ( 3 − z ) ) where 0 ≤ arg ( 3 − z ) < 2 π {\displaystyle (3-z)^{\frac {1}{4}}=\exp \left({\frac {1}{4}}\log(3-z)\right)\quad {\mbox{where}}\quad 0\leq \arg(3-z)<2\pi } となるよう選ぶ。
このとき、z 3/4 の分岐切断は (−∞, 0] であり、(3−z )1/4 の分岐切断は (−∞, 3] となる。これらの積、つまり f (z ) の分岐切断は [0, 3] である。なぜなら、f (z ) は実は (−∞, 0) をまたいで連続になるからである。このことは、z = −r < 0 として (−∞, 0) に向かって上半平面から近づくときの f (z ) の値が
r 3 4 exp ( 3 π i 4 ) ( 3 + r ) 1 4 exp ( 2 π i 4 ) = r 3 4 ( 3 + r ) 1 4 exp ( 5 π i 4 ) {\displaystyle r^{\frac {3}{4}}\exp({\tfrac {3\pi i}{4}})(3+r)^{\frac {1}{4}}\exp({\tfrac {2\pi i}{4}})=r^{\frac {3}{4}}(3+r)^{\frac {1}{4}}\exp({\tfrac {5\pi i}{4}})} であり、一方下半平面から近づくときの f (z ) の値が
r 3 4 exp ( − 3 π i 4 ) ( 3 + r ) 1 4 exp ( 0 π i 4 ) = r 3 4 ( 3 + r ) 1 4 exp ( − 3 π i 4 ) {\displaystyle r^{\frac {3}{4}}\exp(-{\tfrac {3\pi i}{4}})(3+r)^{\frac {1}{4}}\exp({\tfrac {0\pi i}{4}})=r^{\frac {3}{4}}(3+r)^{\frac {1}{4}}\exp(-{\tfrac {3\pi i}{4}})} となるが、
exp ( − 3 π i 4 ) = exp ( 5 π i 4 ) {\displaystyle \exp(-{\tfrac {3\pi i}{4}})=\exp({\tfrac {5\pi i}{4}})} だから、この両者は (−∞, 0) を越えて連続となることからわかる。図中では、2個の向きのついた黒い円周が、それぞれ z 3/4 と (3−z )1/4 を定義している対数関数の偏角とともに示されている。
図中の緑色の積分路を使うことにする。このため線分のすぐ上側と、すぐ下側を通る経路上の積分を考える。これらの経路は極限では(つまり2個の緑色の円周が半径0となるとき)、z = r (0 ≤ r ≤ 3) となる。線分の上側では、f (z ) の値は
r 3 4 exp ( 0 π i 4 ) ( 3 − r ) 1 4 exp ( 2 π i 4 ) = i r 3 4 ( 3 − r ) 1 4 {\displaystyle r^{\frac {3}{4}}\exp({\tfrac {0\pi i}{4}})(3-r)^{\frac {1}{4}}\exp({\tfrac {2\pi i}{4}})=i\,r^{\frac {3}{4}}(3-r)^{\frac {1}{4}}} と求まる。線分の下側では、
r 3 4 exp ( 0 π i 4 ) ( 3 − r ) 1 4 exp ( 0 π i 4 ) = r 3 4 ( 3 − r ) 1 4 {\displaystyle r^{\frac {3}{4}}\exp({\tfrac {0\pi i}{4}})(3-r)^{\frac {1}{4}}\exp({\tfrac {0\pi i}{4}})=r^{\frac {3}{4}}(3-r)^{\frac {1}{4}}} となる。これらより
f ( z ) 5 − z {\displaystyle {\frac {f(z)}{5-z}}} の積分は、線分の上側を通るとき極限では −iI となり、下側を通るとき極限では I となることがわかる。
2個の緑色の円周上の積分が極限では消えることを示せれば、留数定理によって I の値も得られる。緑色の円周の半径を ρ とし、ρ < 1/1000 を満たしつつ ρ → 0 と向かう状況を考える。
ML不等式を左側の円周 CL に適用すると、
| ∫ C L f ( z ) 5 − z d z | ≤ 2 π ρ ρ 3 4 ( 3 + 1 1000 ) 1 4 5 − 1 1000 ∈ O ( ρ 7 4 ) → 0 {\displaystyle \left|\int _{C_{L}}{\frac {f(z)}{5-z}}dz\right|\leq 2\pi \rho {\frac {\rho ^{\frac {3}{4}}(3+{\frac {1}{1000}})^{\frac {1}{4}}}{5-{\frac {1}{1000}}}}\in {\mathcal {O}}\left(\rho ^{\frac {7}{4}}\right)\to 0} が得られる。同様に、右側の円周 C R
| ∫ C R f ( z ) 5 − z d z | ≤ 2 π ρ ( 3 + 1 1000 ) 3 4 ρ 1 4 2 − 1 1000 ∈ O ( ρ 5 4 ) → 0 {\displaystyle \left|\int _{C_{R}}{\frac {f(z)}{5-z}}dz\right|\leq 2\pi \rho {\frac {(3+{\frac {1}{1000}})^{\frac {3}{4}}\rho ^{\frac {1}{4}}}{2-{\frac {1}{1000}}}}\in {\mathcal {O}}\left(\rho ^{\frac {5}{4}}\right)\to 0} が得られる。
ここで留数定理より(今考えている積分路は、内側には有限個の孤立特異点を囲めていない事に注意する)、
( − i + 1 ) I = − 2 π i ( R e s z = 5 f ( z ) 5 − z + R e s z = ∞ f ( z ) 5 − z ) {\displaystyle (-i+1)I=-2\pi i\left(\mathrm {Res} _{z=5}{\frac {f(z)}{5-z}}+\mathrm {Res} _{z=\infty }{\frac {f(z)}{5-z}}\right)} となる。ここで右辺の最初に負号がついているのは、特異点から見ると積分路は時計回りをしているからである。上で定めた対数関数の枝を使うと、明らかに
R e s z = 5 f ( z ) 5 − z = − 5 3 4 exp ( log ( − 2 ) 4 ) . {\displaystyle \mathrm {Res} _{z=5}{\frac {f(z)}{5-z}}=-5^{\frac {3}{4}}\exp \left({\tfrac {\log(-2)}{4}}\right).} この極は図では青い点で示されている。値は単純化されて
− 5 3 4 exp ( log ( 2 ) + π i 4 ) = − exp ( π i 4 ) 5 3 4 2 1 4 {\displaystyle -5^{\frac {3}{4}}\exp \left({\tfrac {\log(2)+\pi i}{4}}\right)=-\exp({\tfrac {\pi i}{4}})5^{\frac {3}{4}}2^{\frac {1}{4}}} となる。
無限遠点での留数を求めるのに、次の公式を使う。
R e s z = ∞ h ( z ) = R e s z = 0 [ − 1 z 2 h ( 1 z ) ] . {\displaystyle \mathrm {Res} _{z=\infty }h(z)=\mathrm {Res} _{z=0}\left[-{\frac {1}{z^{2}}}h\left({\frac {1}{z}}\right)\right].} z を 1/z に置き換えて、
1 5 − 1 z = − z ( 1 + 5 z + 5 2 z 2 + 5 3 z 3 + ⋯ ) {\displaystyle {\frac {1}{5-{\frac {1}{z}}}}=-z\left(1+5z+5^{2}z^{2}+5^{3}z^{3}+\cdots \right)} および
( 1 z 3 ( 3 − 1 z ) ) 1 4 = 1 z ( 3 z − 1 ) 1 4 = 1 z exp ( π i 4 ) ( 1 − 3 z ) 1 4 {\displaystyle \left({\frac {1}{z^{3}}}\left(3-{\frac {1}{z}}\right)\right)^{\frac {1}{4}}={\frac {1}{z}}(3z-1)^{\frac {1}{4}}={\frac {1}{z}}\exp({\tfrac {\pi i}{4}})(1-3z)^{\frac {1}{4}}} を得る。ここで、2番目の対数関数の枝について −1 = e i π
更に二項展開 から、
1 z exp ( π i 4 ) ( 1 − ( 1 4 1 ) 3 z + ( 1 4 2 ) 3 2 z 2 − ( 1 4 3 ) 3 3 z 3 + ⋯ ) {\displaystyle {\frac {1}{z}}\exp({\tfrac {\pi i}{4}})\left(1-{{\frac {1}{4}} \choose 1}3z+{{\frac {1}{4}} \choose 2}3^{2}z^{2}-{{\frac {1}{4}} \choose 3}3^{3}z^{3}+\cdots \right)} を得る。結論として、留数
R e s z = ∞ f ( z ) 5 − z = exp ( π i 4 ) ( 5 − 3 4 ) = exp ( π i 4 ) 17 4 {\displaystyle \mathrm {Res} _{z=\infty }{\frac {f(z)}{5-z}}=\exp({\tfrac {\pi i}{4}})\left(5-{\frac {3}{4}}\right)=\exp({\tfrac {\pi i}{4}}){\frac {17}{4}}} が得られた。
以上より、最終的に I の値は
I = 2 π i exp ( π i 4 ) − 1 + i ( 17 4 − 5 3 4 2 1 4 ) = 2 π 2 − 1 2 ( 17 4 − 5 3 4 2 1 4 ) = π 2 2 ( 17 − 5 3 4 2 9 4 ) = π 2 2 ( 17 − 40 3 4 ) {\displaystyle {\begin{aligned}I&=2\pi i{\frac {\exp({\tfrac {\pi i}{4}})}{-1+i}}\left({\frac {17}{4}}-5^{\frac {3}{4}}2^{\frac {1}{4}}\right)=2\pi 2^{-{\frac {1}{2}}}\left({\frac {17}{4}}-5^{\frac {3}{4}}2^{\frac {1}{4}}\right)\\&={\frac {\pi }{2{\sqrt {2}}}}\left(17-5^{\frac {3}{4}}2^{\frac {9}{4}}\right)={\frac {\pi }{2{\sqrt {2}}}}\left(17-40^{\frac {3}{4}}\right)\end{aligned}}} と求まる。
積分表現 詳細は「積分表現」を参照
関数の積分表現 (integral representation) とは路に沿う積分を含む関数の表示である。様々な積分表現が多くの特殊関数 に対して知られている。積分表現は理論的な理由で重要となり得る。例えば解析接続 や関数等式 やときには数値評価を与える。
ハンケルの積分路 例えば、リーマンのゼータ関数 ζ (s )ディリクレ級数 を用いたもともとの定義
∑ n = 1 ∞ 1 n s {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{s}}}} は Re(s ) > 1 に対してのみ有効である。しかし
ζ ( s ) = − Γ ( 1 − s ) 2 π i ∫ H ( − t ) s − 1 e t − 1 d t {\displaystyle \zeta (s)=-{\frac {\Gamma (1-s)}{2\pi i}}\int _{H}{\frac {(-t)^{s-1}}{e^{t}-1}}dt} (ただし積分はハンケルの積分路(英語版) H 上する)はすべての複素数 s に対して有効である。
関連項目 出典 ^ John Stalker (1998). Complex Analysis: Fundamentals of the Classical Theory of Functions . Springer. p. 77. ISBN 0-8176-4038-X. https://books.google.com/books?id=yl3GIXd3dFIC&pg=PP12&dq=%22calculus+of+residues%22#PPA77,M1 ^ Joseph Bak & Donald J. Newman (1997). Complex Analysis . Springer. Chapters 11 & 12, pp. 130–156. ISBN 0-387-94756-6. https://books.google.com/books?id=JX2YSgfZwbYC&pg=PA130&dq=%22contour+integral%22#PPA130,M1 ^ Steven George Krantz (1999). “Chapter 2”. Handbook of Complex Variables . Springer. ISBN 0-8176-4011-8. https://books.google.com/books?id=aYU2AdF_0dIC&pg=PT13&dq=Calculus++Residues+inauthor:krantz#PPT47,M1 ^ Dragoslav S. Mitrinovic & Jovan D. Keckic (1984). “Chapter 2”. The Cauchy Method of Residues: Theory and Applications . Springer. ISBN 90-277-1623-4. https://books.google.com/books?id=-suKhxfPH5AC&printsec=frontcover&dq=%22calculus+of+residues%22#PPA5,M1 ^ Dragoslav S. Mitrinovic & Jovan D. Keckic (1984). Chapter 5 . ISBN 90-277-1623-4. https://books.google.com/books?id=-suKhxfPH5AC&printsec=frontcover&dq=%22calculus+of+residues%22#PPA108,M1 ^ a b c d e Edward B. Saff & Arthur David Snider (2003). Chapter 4 . ISBN 01-390-7874-6. https://books.google.com/books?id=fVsZAQAAIAAJ&q=saff+%26+Snider&dq=saff+%26+Snider&hl=en&sa=X&ei=rT7PUPaiL4OE2gXvg4GoBQ&ved=0CFEQ6AEwAw 注釈 ^ (訳注)実軸に平行な路に沿った複素線積分の収束性については、厳密にはもう少し議論が要るように思われる(これに続く例でも同様)。 この箇所の実軸下側の複素線積分について述べれば、例えば、n を自然数、x ∈ [0, +∞)、1A (・) を指示関数 として e 1 2 log | x − i n | e ( i / 2 ) arg ( x − i n ) ( x − i n ) 2 + 6 ( x − i n ) + 8 ⋅ 1 [ 1 n , n ] ( x ) {\displaystyle {e^{{1 \over 2}\log {|x-{\frac {i}{n}}|}}e^{(i/2)\arg {(x-{\frac {i}{n}})}} \over (x-{\frac {i}{n}})^{2}+6(x-{\frac {i}{n}})+8}\cdot 1_{[{\frac {1}{n}},n]}(x)} n によらずに [0, +∞) 上可積分かつ、可積分関数 e 1 2 log | x + 1 | x 2 + 6 x + 8 {\displaystyle {e^{{1 \over 2}\log {|x+1|}} \over x^{2}+6x+8}} n → ∞ のとき − x x 2 + 6 x + 8 {\displaystyle {-{\sqrt {x}} \over x^{2}+6x+8}} 優収束定理 により、本文で述べているような変形が正当化される。 関連文献 Titchmarsh, E.C. (1939), The Theory of Functions (2nd ed.), Oxford University Press , ISBN 0-19-853349-7 Jean Jacquelin, Marko Riedel, Branche univalente, Les-Mathematiques.net , in French. Marko Riedel et al., Problème d'intégrale, Les-Mathematiques.net , in French. Marko Riedel et al., Integral by residue, math.stackexchange.com . Various authors, sin límites ni cotas, es.ciencia.matematicas , in Spanish. W W L Chen, Introduction to Complex Analysis 外部リンク Hazewinkel, Michiel, ed. (2001), “Complex integration, method of”, Encyclopedia of Mathematics , Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Complex_integration,_method_of A collection of examples Residue Calculus Module by John H. Mathews 積分法 計算法 部分積分 置換積分 逆函数の積分(英語版) 積分の順序(英語版) 三角函数置換(英語版) 部分分数分解を通じた積分(英語版) 漸化式による積分 媒介変数微分を用いた積分(英語版) オイラーの公式を用いた積分(英語版) 積分記号下の微分(英語版) 複素線積分 広義積分 確率積分 伊藤積分(英語版) ストラトノヴィッチ積分(英語版) スコロホッド積分(英語版) 数値積分 積分方程式








![{\displaystyle {\begin{aligned}\int _{a}^{b}f(t)\,dt&=\int _{a}^{b}{\big [}u(t)+iv(t){\big ]}\,dt\\&=\int _{a}^{b}u(t)\,dt+i\int _{a}^{b}v(t)\,dt.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3daaf6e0888368de4434a7a375d8e8e6df2f8d3)





























![{\displaystyle {\begin{aligned}&-{\frac {4}{3}}i\left[\oint _{C_{1}}{\frac {\frac {z}{(z+{\sqrt {3}}i)(z-{\sqrt {3}}i)\left(z+{\frac {i}{\sqrt {3}}}\right)}}{z-{\frac {i}{\sqrt {3}}}}}\,dz+\oint _{C_{2}}{\frac {\frac {z}{(z+{\sqrt {3}}i)(z-{\sqrt {3}}i)\left(z-{\frac {i}{\sqrt {3}}}\right)}}{z+{\frac {i}{\sqrt {3}}}}}\,dz\right]\\&=-{\frac {4}{3}}i\left[2\pi i\left({\frac {z}{(z+{\sqrt {3}}i)(z-{\sqrt {3}}i)(z+{\frac {i}{\sqrt {3}}})}}\right){\Bigg |}_{z={\frac {i}{\sqrt {3}}}}+2\pi i\left({\frac {z}{(z+{\sqrt {3}}i)(z-{\sqrt {3}}i)(z-{\frac {i}{\sqrt {3}}})}}\right){\Bigg |}_{z=-{\frac {i}{\sqrt {3}}}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{({\frac {i}{\sqrt {3}}}+{\sqrt {3}}i)({\frac {i}{\sqrt {3}}}-{\sqrt {3}}i)({\frac {i}{\sqrt {3}}}+{\frac {i}{\sqrt {3}}})}}+{\frac {-{\frac {i}{\sqrt {3}}}}{(-{\frac {i}{\sqrt {3}}}+{\sqrt {3}}i)(-{\frac {i}{\sqrt {3}}}-{\sqrt {3}}i)(-{\frac {i}{\sqrt {3}}}-{\frac {i}{\sqrt {3}}})}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{({\frac {4}{\sqrt {3}}}i)(-{\frac {2}{i{\sqrt {3}}}})({\frac {2}{{\sqrt {3}}i}})}}+{\frac {-{\frac {i}{\sqrt {3}}}}{({\frac {2}{\sqrt {3}}}i)(-{\frac {4}{\sqrt {3}}}i)(-{\frac {2}{\sqrt {3}}}i)}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{i({\frac {4}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})}}+{\frac {-{\frac {i}{\sqrt {3}}}}{-i({\frac {2}{\sqrt {3}}})({\frac {4}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {1}{\sqrt {3}}}{({\frac {4}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})}}+{\frac {\frac {1}{\sqrt {3}}}{({\frac {2}{\sqrt {3}}})({\frac {4}{\sqrt {3}}})({\frac {2}{\sqrt {3}}})}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {\frac {1}{\sqrt {3}}}{\frac {16}{3{\sqrt {3}}}}}+{\frac {\frac {1}{\sqrt {3}}}{\frac {16}{3{\sqrt {3}}}}}\right]\\&={\frac {8\pi }{3}}\left[{\frac {3}{16}}+{\frac {3}{16}}\right]=\pi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337bba7c71f225f172b8d680a9b40f924e37a719)










































![{\displaystyle \mathrm {Res} _{z=\infty }h(z)=\mathrm {Res} _{z=0}\left[-{\frac {1}{z^{2}}}h\left({\frac {1}{z}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4613847fb0db7551db4310746bff50ea2af89663)







![{\displaystyle {e^{{1 \over 2}\log {|x-{\frac {i}{n}}|}}e^{(i/2)\arg {(x-{\frac {i}{n}})}} \over (x-{\frac {i}{n}})^{2}+6(x-{\frac {i}{n}})+8}\cdot 1_{[{\frac {1}{n}},n]}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ed3daa19871026d7bce15bc6a89cdcf17f1f578)








