Kondensat Bosego-Einsteina
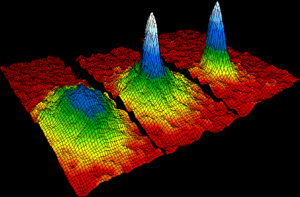
Kondensacja Bosego-Einsteina – efekt kwantowy zachodzący w układach podległych rozkładowi Bosego-Einsteina. W temperaturach niższych od temperatury krytycznej część cząstek (bozonów) przechodzi w zerowy stan pędowy – cząstki te mają identyczny pęd. Oznacza to, że w zerowej objętości przestrzeni pędów może znajdować się niezerowa liczba cząstek. Mówi się wtedy o makroskopowym obsadzeniu stanu podstawowego.
Efektem kondensacji jest kolektywne zachowanie wszystkich cząstek biorących w niej udział (w przybliżeniu wszystkie zachowują się jak jedna cząstka). Nie chodzi tu o kondensację w zwykłym sensie w przestrzeni położeń – cząstki nie znajdują się w jednym miejscu, lecz o „kondensację” cząstek w przestrzeni pędów – znaczna liczba cząstek ma taki sam pęd. Rozkład przestrzenny cząstek „skondensowanych” pozostaje równomierny (jeśli nie ma pól zewnętrznych). W kondensacie Bosego-Einsteina zachodzi zjawisko nadciekłości. Kondensat opisywany jest w przybliżeniu nieliniowym równaniem Grossa-Pitajewskiego. Równanie to ma rozwiązania solitonowe, o wielkim znaczeniu eksperymentalnym. Występują zarówno „jasne”, jak i „ciemne” rozwiązania solitonowe. Przybliżenie można polepszyć stosując rachunek zaburzeń – teorię Bogolubowa.
Historia

Zjawisko przewidziane przez indyjskiego fizyka Satyendrę Natha Bosego i Alberta Einsteina w 1924, a po raz pierwszy zaobserwowane w 1995 dla rzadkiego, alkalicznego metalu – rubidu-87 (87Rb) – przez zespół badawczy z JILA w Boulder (Kolorado) Erica Cornella i Carla Wiemana[1]. Kondensat Bosego-Einsteina otrzymał również w tym samym czasie zespół Wolfganga Ketterlego z MIT, który zaobserwował kondensację sodu-23 (23Na)[2]. Eric Cornell, Wolfgang Ketterle i Carl Wieman za swoje pionierskie badania i otrzymanie po raz pierwszy kondensatu, w 2001 roku zostali nagrodzeni Nagrodą Nobla w dziedzinie fizyki. W ciągu kolejnych lat udało się również otrzymać kondensaty Bosego-Einsteina gazów takich izotopów jak 7Li, 23Na, 39K, 41K, 85Rb, 87Rb, 133Cs, 52Cr, 40Ca, 84Sr, 88Sr i 174Yb.
Stosując technikę magnetoasocjacji w 2003 roku otrzymano pierwsze kondensaty Bosego-Einsteina cząsteczek (Li2[3][4], i K2[5]), przy czym były to kondensaty słabo związanych cząsteczek Feshbacha.
Pierwszy polski kondensat rubidu-87 otrzymany został 2 marca 2007 roku w Krajowym Laboratorium Fizyki Atomowej, Molekularnej i Optycznej (KL FAMO) w Toruniu, z wykorzystaniem aparatury skonstruowanej przez grupę Wojciecha Gawlika w Zakładzie Fotoniki Instytutu Fizyki Uniwersytetu Jagiellońskiego w Krakowie (budowa aparatury próżniowej i toru optycznego oraz uruchomienie dwóch pułapek magnetooptycznych) oraz grupę Włodzimierza Jastrzębskiego w Instytucie Fizyki PAN w Warszawie (pułapka magnetyczna), a następnie przewiezionej do KL FAMO[6].
Ujęcie matematyczne
Liczba cząstek znajdujących się w stanie podstawowym zależy od warunków fizycznych, w jakich doprowadza się do kondensacji. Dla gazu swobodnego wzór jako pierwsi znaleźli właśnie Bose i Einstein, i ma on postać:
W sytuacji bardziej realistycznej, gdy układ znajduje się w pułapce harmonicznej, zależność ta ma postać:
gdzie:
- – liczba cząstek, która uległa kondensacji,
- – całkowita liczba cząstek,
- – temperatura kondensatu,
- – temperatura krytyczna.
Dla innych sytuacji fizycznych, tzw. wykładnik krytyczny (potęga przy stosunku temperatury do temperatury krytycznej) może być inny. Powyżej temperatury krytycznej nie ma makroskopowego obsadzenia stanu podstawowego i gaz zachowuje się prawie jak gaz doskonały z małymi poprawkami wynikającymi ze statystyki kwantowej.
Kondensacja Bosego-Einsteina w kulturze
- film Spectral(inne języki) (2016) – proces kondensacji Bosego-Einsteina jest używany jako wyjaśnienie na jakiej podstawie powstają zjawy, które zabijają ludzi w filmie[7].
Przypisy
- ↑ M.H.M.H. Anderson M.H.M.H. i inni, Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor, „Science”, 269 (5221), 1995, s. 198–201, DOI: 10.1126/science.269.5221.198, PMID: 17789847 (ang.).
- ↑ K.B.K.B. Davis K.B.K.B. i inni, Bose-Einstein Condensation in a Gas of Sodium Atoms, „Physical Review Letters”, 75 (22), 1995, s. 3969–3973, DOI: 10.1103/PhysRevLett.75.3969 (ang.).
- ↑ S.S. Jochim S.S., Bose-Einstein Condensation of Molecules, „Science”, 302 (5653), 2003, s. 2101–2103, DOI: 10.1126/science.1093280, PMID: 14615548 (ang.).
- ↑ M.W.M.W. Zwierlein M.W.M.W. i inni, Observation of Bose-Einstein Condensation of Molecules, „Physical Review Letters”, 91 (25), 2003, DOI: 10.1103/PhysRevLett.91.250401 (ang.).
- ↑ MarkusM. Greiner MarkusM., Cindy A.C.A. Regal Cindy A.C.A., Deborah S.D.S. Jin Deborah S.D.S., Emergence of a molecular Bose–Einstein condensate from a Fermi gas, „Nature”, 426 (6966), 2003, s. 537–540, DOI: 10.1038/nature02199, PMID: 14647340 (ang.).
- ↑ W.W. Gawlik W.W. i inni, Pierwszy polski kondensat Bosego-Einsteina, „Postępy Fizyki”, 58 (4), 2007, s. 156 [zarchiwizowane z adresu 2016-03-05] .
- ↑ ArsA. Staff ArsA., The science of Spectral: Is that really how Bose–Einstein condensate behaves? [online], Ars Technica, 18 lipca 2017 [dostęp 2021-04-20] (ang.).
Linki zewnętrzne
- KrzysztofK. Byczuk KrzysztofK., Obserwacja kondensacji Bosego-Einsteina, [w:] pismo „Delta”, deltami.edu.pl, październik 1996, ISSN 0137-3005 [dostęp 2024-03-25] (pol.).
- KrzysztofK. Pawłowski KrzysztofK., Krople kwantowe, [w:] pismo „Delta”, deltami.edu.pl, marzec 2021, ISSN 0137-3005 [dostęp 2021-09-14] (pol.). – artykuł o różnych formach kondensatu, w tym kroplach i supersolidach.
- Britannica: science/Bose-Einstein-condensate
- Universalis: condensation-de-bose-einstein
- БРЭ: 1869523
- NE.se: bose-einstein-kondensat
- SNL: Bose-Einsteinkondensat
![{\displaystyle N_{0}=N\left[1-\left({\frac {T}{T_{C}}}\right)^{\frac {3}{2}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dad642884d0480ee4754b994b3380b6c54ee3d8)
![{\displaystyle N_{0}=N\left[1-\left({\frac {T}{T_{C}}}\right)^{3}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91b1925e9d3184272d60ab74482ae5a78497b50c)














