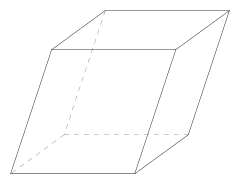
平行六面体

平行六面体（へいこうろくめんたい、parallelepiped）とは、6面の平行四辺形で構成されている立体であり、ゾーン多面体、平行多面体の一種である。

性質

平行六面体は異なる36種類の展開図がある。^[1]

特殊な場合

全てのとなり合う面が直交し、従って、6面がすべて長方形である場合には直方体となる。

6面がすべて合同の正方形でない菱形であるような平行六面体は特に菱面体（英語版）と呼ばれ、2つの頂点に3つの菱形の鋭角が集まるもの(acute)と、鈍角が集まるもの(obtuse)の2種類がある。後者は鈍角の角度が120度以下でなければならない。

直方体であり、かつ、菱面体である場合が、立方体である。

体積

一つの面を水平面に置くと、体積は、（一つの）水平面（それぞれ平行四辺形である）の面積に高さを掛け算したものになる。ここに、高さとは必ずしもある辺の長さではなく、水平面に垂直の軸に沿って計測されるものである。

あるいは、平行六面体の中心を座標原点に置いたときの８個の頂点の座標を ui で表すなら、体積は次式で与えることもできる。この場合は、図形の置かれる角度は問わない。

${\textstyle V={\sqrt {{\frac {1}{8}}{\begin{vmatrix}\sum _{i=1}^{8}\mathbf {u_{i}} \otimes \mathbf {u_{i}} \end{vmatrix}}}}={\sqrt {{\frac {1}{8}}{\begin{vmatrix}\sum _{i=1}^{8}\mathbf {u_{i}} \mathbf {u_{i}} ^{\top }\end{vmatrix}}}}={\sqrt {{\frac {1}{8}}{\begin{vmatrix}\sum _{i=1}^{8}{\begin{pmatrix}u_{x}\\u_{y}\\u_{z}\end{pmatrix}}_{i}{\begin{pmatrix}u_{x}&u_{y}&u_{z}\end{pmatrix}}_{i}\end{vmatrix}}}}}$

${\textstyle ={\sqrt {{\frac {1}{8}}{\begin{vmatrix}\sum _{i=1}^{8}{\begin{pmatrix}u_{x}u_{x}&u_{x}u_{y}&u_{x}u_{z}\\u_{y}u_{x}&u_{y}u_{y}&u_{y}u_{z}\\u_{z}u_{x}&u_{z}u_{y}&u_{z}u_{z}\end{pmatrix}}_{i}\end{vmatrix}}}}}$

${\textstyle ={\sqrt {{\frac {1}{8}}{\begin{vmatrix}\sum _{i=1}^{8}u_{ix}u_{ix}&\sum _{i=1}^{8}u_{ix}u_{iy}&\sum _{i=1}^{8}u_{ix}u_{iz}\\\sum _{i=1}^{8}u_{iy}u_{ix}&\sum _{i=1}^{8}u_{iy}u_{iy}&\sum _{i=1}^{8}u_{iy}u_{iz}\\\sum _{i=1}^{8}u_{iz}u_{ix}&\sum _{i=1}^{8}u_{iz}u_{iy}&\sum _{i=1}^{8}u_{iz}u_{iz}\end{vmatrix}}}}}$

脚注

表 話 編 歴 多面体
一様多面体	正多面体 正四面体 正六面体 正八面体 正十二面体 正二十面体 半正多面体 切頂四面体 切頂六面体 切頂八面体 切頂十二面体 切頂二十面体 立方八面体 二十・十二面体 斜方立方八面体 斜方二十・十二面体 斜方切頂立方八面体 斜方切頂二十・十二面体 変形立方体 変形十二面体 星型正多面体 小星型十二面体 大十二面体 大星型十二面体 大二十面体 その他 八面半八面体 四面半六面体 小立方立方八面体 大立方立方八面体 立方半八面体 立方切頂立方八面体 一様大斜方立方八面体 小斜方六面体 星型切頂六面体 大切頂立方八面体 大斜方六面体 小二重三角二十・十二面体 小二十・二十・十二面体 小変形二十・二十・十二面体 小十二・二十・十二面体 十二・十二面体 切頂大十二面体 斜方十二・十二面体 小斜方十二面体 変形十二・十二面体 二重三角十二・十二面体 大二重三角十二・二十・十二面体 小二重三角十二・二十・十二面体 二十・十二・十二面体 二十面切頂十二・十二面体 変形二十・十二・十二面体 大二重三角二十・十二面体 大二十・二十・十二面体 小二十面半十二面体 小十二・二十面体 小十二面半十二面体 大二十・十二面体 切頂大二十面体 斜方二十面体 大変形二十・十二面体 小星型切頂十二面体 切頂十二・十二面体 逆変形十二・十二面体 大十二・二十・十二面体 小十二面半二十面体 大十二・二十面体 大変形十二・二十・十二面体 大十二面半二十面体 大星型切頂十二面体 一様大斜方二十・十二面体 大切頂二十・十二面体 大逆変形二十・十二面体 大十二面半十二面体 大二十面半十二面体 小反屈変形二十・二十・十二面体 大斜方十二面体 大反屈変形二十・十二面体 大二重斜方二十・十二面体
カタランの立体	三方四面体 三方八面体 四方六面体 三方二十面体 五方十二面体 菱形十二面体 菱形三十面体 凧形二十四面体 凧形六十面体 六方八面体 六方二十面体 五角二十四面体 五角六十面体
ジョンソンの立体	正四角錐 正五角錐 正三角台塔 正四角台塔 正五角台塔 正五角丸塔 正三角錐柱 正四角錐柱 正五角錐柱 正四角錐反柱 正五角錐反柱 双三角錐 双五角錐 双三角錐柱 双四角錐柱 双五角錐柱 双四角錐反柱 正三角台塔柱 正四角台塔柱 正五角台塔柱 正五角丸塔柱 正三角台塔反柱 正四角台塔反柱 正五角台塔反柱 正五角丸塔反柱 異相双三角柱 同相双三角台塔 同相双四角台塔 異相双四角台塔 同相双五角台塔 異相双五角台塔 同相五角台塔丸塔 異相五角台塔丸塔 同相双五角丸塔 同相双三角台塔柱 異相双三角台塔柱 異相双四角台塔柱 同相双五角台塔柱 異相双五角台塔柱 同相五角台塔丸塔柱 異相五角台塔丸塔柱 同相双五角丸塔柱 異相双五角丸塔柱 双三角台塔反柱 双四角台塔反柱 双五角台塔反柱 五角台塔丸塔反柱 双五角丸塔反柱 側錐三角柱 二側錐三角柱 三側錐三角柱 側錐五角柱 二側錐五角柱 側錐六角柱 双側錐六角柱 二側錐六角柱 三側錐六角柱 側錐十二面体 双側錐十二面体 二側錐十二面体 三側錐十二面体 二側錐欠損二十面体 三側錐欠損二十面体 側錐三側錐欠損二十面体 側台塔切頂四面体 側台塔切頂立方体 双側台塔切頂立方体 側台塔切頂十二面体 双側台塔切頂十二面体 二側台塔切頂十二面体 三側台塔切頂十二面体 側台塔回転斜方二十・十二面体 双側台塔回転斜方二十・十二面体 二側台塔回転斜方二十・十二面体 三側台塔回転斜方二十・十二面体 側台塔欠損斜方二十・十二面体 双側台塔回転欠損斜方二十・十二面体 二側台塔回転欠損斜方二十・十二面体 二側台塔回転側台塔欠損斜方二十・十二面体 双側台塔欠損斜方二十・十二面体 二側台塔欠損斜方二十・十二面体 側台塔回転二側台塔欠損斜方二十・十二面体 三側台塔欠損斜方二十・十二面体 変形双五角錐 変形四角反柱 球形屋根 側錐球形屋根 長球形屋根 広底長球形屋根 五角錐球形屋根 双三日月双丸塔 三角広底球形屋根丸塔
ゾーン多面体	平行六面体 菱形十二面体第2種 菱形二十面体 菱形九十面体 長菱形十二面体
星型多面体	小三角六辺形二十面体 完全二十面体 星型八面体
ねじれ正多面体	四角六片四角孔ねじれ正多面体 六角四片四角孔ねじれ正多面体 六角六片三角孔ねじれ正多面体
面の数による分類	二面体 四面体 五面体 六面体 七面体 八面体 十面体 十二面体 十四面体 二十面体 二十四面体 三十面体 四十八面体 六十面体 百二十面体
その他	角錐 角柱 双角錐 反角柱 ねじれ双角錐 プリズマトイド（英語版） 擬大斜方立方八面体 大二重変形二重斜方十二面体 切稜立方体 穿孔多面体 ダ・ヴィンチの星 正四面体リング 凸多面体 凹多面体 双対多面体 複合多面体 平面充填形