円の面積(えんのめんせき) は、円周率を
は、円周率を  、円の半径を
、円の半径を  としたとき、
としたとき、

で表される。
歴史
古代エジプト
 円の直径から、その1/9を引いたものを2乗すると円の面積になる(リンド・パピルス)
円の直径から、その1/9を引いたものを2乗すると円の面積になる(リンド・パピルス) 古代エジプトにおいては、リンド・パピルスの問題50に円の面積を求める方法が記録されている[注釈 1]。
リンド・パピルスでは、円の直径  [注釈 2]からその
[注釈 2]からその  を引いた数の2乗、
を引いた数の2乗、

として円の面積を求めている。これは半径  を用いて書き直せば、
を用いて書き直せば、

となる。したがって、現代の視点ではリンド・パピルスにおける計算は円周率を

と近似したものと見なせる。ただしこのことは、古代エジプト人が円周率を知っていたことや円周率の近似値を種々の計算に利用していたことを直ちに意味しない。
古代バビロニア
バビロニア数学では、円周の長さを  としたとき、
としたとき、

で求めていた。また、円周率に相当する数値は、円に内接する正6角形によって近似した 3 や、内接および外接する正12角形で円の面積を近似して求まる 3.125 であったといわれている。
ヘブライ
ヘブライ語最古とされる幾何学書『ミシュナート・ハ・ミッドット(英語版)』によれば、円の直径  の自乗からその
の自乗からその  と
と  を取り去ると円の面積
を取り去ると円の面積  が得られる。これは、
が得られる。これは、

である。したがって、半径  で整理すれば、
で整理すれば、

となり、円周率に相当する数値は  と求まる。
と求まる。
古代ギリシャ
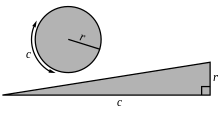 円の面積は、円周 c を底辺、半径 r を高さとする直角三角形の面積に等しい
円の面積は、円周 c を底辺、半径 r を高さとする直角三角形の面積に等しい エウクレイデスは『原論』において、直径  の円の面積が1辺を
の円の面積が1辺を  とする 正方形の面積に比例することを証明した。しかし、円周率の値には言及していなかった。
とする 正方形の面積に比例することを証明した。しかし、円周率の値には言及していなかった。
 円に内接する正6,12,24角形
円に内接する正6,12,24角形 アルキメデスは『円の計測』において、
- 命題1
- 円の面積は、円周の長さを底辺、半径を高さとする直角三角形の面積に等しい
- 命題3
- 円周と直径との比は、
 より大きく、
より大きく、 より小さい[注釈 3]
より小さい[注釈 3]
を、取り尽くし法を用いて証明した。命題1は、円に内接および外接する正方形(正4角形)から辺数を増やしていき、円の面積が円周の長さを底辺、半径を高さとする直角三角形の面積よりも「大きくなく」「小さくない」ことで等しいことを証明[注釈 4]した。命題3は、円に内接する正多角形の辺長と外接する正多角形の辺長の間に円周の長さがあることを用いて、円に内接および外接する正6角形から出発して正96角形で証明した。
古代中国
 『九章算術』劉徽による円に内接する正多角形を用いた円の求積
『九章算術』劉徽による円に内接する正多角形を用いた円の求積 『九章算術』に註釈をつけた魏の劉徽は、円の内接する正6角形から正12角形、正24角形と辺数を増やしていくと、やがて内接多角形の面積は円の面積に差は無くなる、としている。
具体的には、円に内接する正n多角形のうち1つの三角形(△OAB)に対し、三角形の底辺とそのの二等分線と円周上の交点を高さとする長方形で囲まれる面積(□AA'B'B)を考えると、内接する正n角形の面積とその面積に長方形の面積を加えたものの間に円の面積がある、ということを利用している(右図)。
正n角形の面積を 、円の面積を
、円の面積を としたとき、
としたとき、

となり、半径10の円に対する正192角形までを評価して[注釈 5]、  を得た。 さらに内接多角形の辺を増やしていくことによって、
を得た。 さらに内接多角形の辺を増やしていくことによって、 を得ている[19]。
を得ている[19]。
日本
江戸時代初期に発行された算術書である吉田光由の『塵劫記』において、直径  の円の面積は、直径の自乗に「まるき法」を掛けて求める。ここで、まるき法は
の円の面積は、直径の自乗に「まるき法」を掛けて求める。ここで、まるき法は に相当する値で、0.79 である。面積
に相当する値で、0.79 である。面積  で表せば、
で表せば、

である。
また、円周の長さ  の円の面積は、円周の長さを「円きめくり法」で割り、直径
の円の面積は、円周の長さを「円きめくり法」で割り、直径  を求めてから上記の方法を使って円の面積を求める。ここで、円きめくり法は円周率に相当する値で、3.16 である。面積
を求めてから上記の方法を使って円の面積を求める。ここで、円きめくり法は円周率に相当する値で、3.16 である。面積  で表せば、
で表せば、

である。
円の面積の公式の導出
アルキメデスによる証明から、命題1における円周の長さを  、半径を
、半径を  とすると、円の面積
とすると、円の面積  は底辺が
は底辺が  、高さが
、高さが  の直角三角形の面積なので、
の直角三角形の面積なので、

となる。 命題3における円周の長さ  と直径の比を
と直径の比を  とすれば、直径は半径の2倍の
とすれば、直径は半径の2倍の  なので、
なので、

であり、  を
を に代入すると、
に代入すると、

となり、円の面積の公式が得られる。
円の面積を求める他の方法
幾何学的変形
 半径
半径 の円を放射状に切断し交互に並べると、縦が半径
の円を放射状に切断し交互に並べると、縦が半径 、横が
、横が の長方形と見なせる。
の長方形と見なせる。 - 変形方法(1)
半径rの円を中心から扇形に細かく等分し、右図のように半分を互いに櫛形に合わさるように組み合わせる。非常に細かく等分していけば、横の長さは円周の長さの半分、縦の長さは半径とみなせるので、それぞれ  、
、 の長方形の面積になる。したがって、
の長方形の面積になる。したがって、

となる[注釈 6]。
 半径
半径 の円を放射状に切断し円周を直線状に延ばすと、円を分割した三角形を並べたものと見なせる。
の円を放射状に切断し円周を直線状に延ばすと、円を分割した三角形を並べたものと見なせる。 - 変形方法(2)
半径rの円を中心から扇形に細かく等分し、円周を直線に延ばすと、直線上には切断した扇形(三角形)が並び、その高さは全て半径rに等しい。円の中心にあった頂点を平行移動して一点に集めても面積は変わらないので、底辺が円周に等しい  、高さが半径
、高さが半径  に等しい三角形の面積であり、
に等しい三角形の面積であり、

が得られる。
円に内接または外接する正多角形の面積の極限
円に内接または外接する正多角形(正n角形)の辺数nを増やしていくと円の面積に等しくなる。
内接正多角形
 円に内接/外接する正多角形の面積を求める
円に内接/外接する正多角形の面積を求める 半径rの円に内接する正n角形において、1区画の三角形の面積を考える(右図(a))。
三角形の高さは  、底辺は
、底辺は  となるので、1区画の面積は
となるので、1区画の面積は  であり、全区画の合計は
であり、全区画の合計は  である。
である。
したがって、 とすれば、
とすれば、

ここで、 とおけば、
とおけば、

さらに、 なので、
なので、

である。
外接正多角形
内接正多角形と同様に1区画の三角形の面積を考える(右図(b))
三角形の高さは  、底辺は
、底辺は  となるので、1区画の面積は
となるので、1区画の面積は  であり、全区画の合計は
であり、全区画の合計は  である。
である。
 とすれば、
とすれば、 であるから、
であるから、

これは内接正多角形の場合と同様の式であり、上式は  に等しくなる。
に等しくなる。
積分
デカルト座標の原点における半径 r の円の方程式  に対し、四分円
に対し、四分円 
 の面積
の面積  を考え、結果を4倍すれば円の面積が求まる。
を考え、結果を4倍すれば円の面積が求まる。
部分積分による計算

において、 、
、 とおけば、
とおけば、 の原始関数は
の原始関数は 、
、 であるから、部分積分の公式
であるから、部分積分の公式 を用いて、
を用いて、

が得られるので、四分円の定積分は、
![{\displaystyle {\begin{aligned}S_{4}&=\int _{0}^{r}{\sqrt {r^{2}-x^{2}}}\,dx\\&=\left[{\frac {1}{2}}(x{\sqrt {r^{2}-x^{2}}}+r^{2}\arcsin {\frac {x}{r}})\right]_{0}^{r}\\&={\frac {\pi r^{2}}{4}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75c9bfd2798b812d28a0fce06c0ba92da4585f05)
である。したがって、全円の面積 S は  なので、
なので、

になる。
三角関数による置換積分
四分円の定積分は、

ここで、 とおけば、
とおけば、 、積分範囲は
、積分範囲は  から
から  となる。また、
となる。また、 となるので、
となるので、
![{\displaystyle {\begin{aligned}S_{4}&=\int _{0}^{\frac {\pi }{2}}r^{2}\cos ^{2}t\,dt\\&=r^{2}\int _{0}^{\frac {\pi }{2}}{\frac {1+\cos 2t}{2}}\,dt\\&={\frac {r^{2}}{2}}\left[t+{\frac {\sin 2t}{2}}\right]_{0}^{\frac {\pi }{2}}\\&={\frac {\pi r^{2}}{4}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12a359b57d4f1b1fe4898a8c008e66eac8c06ad4)
である。全円の面積 S は  なので、
なので、

になる。
リーマン和による求積(区分求積法)
関数  を考えたとき、この関数は
を考えたとき、この関数は  において連続であるからリーマン和による面積の計算が可能であり、それは上記の定積分と等しくなる。
において連続であるからリーマン和による面積の計算が可能であり、それは上記の定積分と等しくなる。
 において、区間
において、区間 ![{\displaystyle [0,r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e37e877243c4e605346083360f52c6faea13009e) を n分割する
を n分割する  、
、 、
、 をとり、区間
をとり、区間 ![{\displaystyle [x_{k-1},x_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f77539e232b976d1a83e1829624235bba4164757) における任意の点を
における任意の点を  とすれば、四分円のリーマン和は、
とすれば、四分円のリーマン和は、

である[注釈 7]。
ここで、分割方法をn等分とすれば、 であり、
であり、 とおくと、
とおくと、

さらに、

であるから[注釈 8]、

となって、 を得る。
を得る。
円環の積分による求積
 円環の積分による円の求積
円環の積分による円の求積 原点を中心として、半径  の円周 (
の円周 ( ) に対して、高さ
) に対して、高さ  の円環を考える。
の円環を考える。
このとき、 が小さければ、半径
が小さければ、半径  の円周と高さ
の円周と高さ  でできる面積は長方形とみなせ、その面積は
でできる面積は長方形とみなせ、その面積は  である。したがって、半径
である。したがって、半径  の円の面積は
の円の面積は  を 0 から
を 0 から  まで積分したものに等しい。
まで積分したものに等しい。
![{\displaystyle {\begin{aligned}S=\int _{0}^{r}\,dS&=\int _{0}^{r}2\pi x\,dx\\&=2\pi \left[{\frac {x^{2}}{2}}\right]_{0}^{r}\\&=\pi r^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c8c2c2489681c9c3719c546c339c73839d915b7)
日本の算数数学教育における循環論法
小学校において円の面積の公式が導入された後、高校の数学Ⅲの課程において「いろいろな曲線で囲まれた図形の面積」[34]を積分法によって導出することが可能になるが、この一連の流れは循環論法をなしていることが指摘されている[35][36]。
循環論法の流れ (山川 2007に基づく)
- 円の面積の公式 S = πr2 から、中心角 θ (rad) の扇形の面積は 1/2πr2θ である。
- 中心角 θ (rad) の扇型の面積を用いて、不等式 1/2r2sin θ < 1/2r2θ < 1/2r2tan θ が導出される。
- はさみうちの原理により、limθ → 0sin θ/θ = 1 が導出される。
- limθ → 0sin θ/θ = 1 より、d/dx(sin x) = cos x である。
- sin x の微分が cos x であることを用いて、
 を得る。従って S = πr2 である。
を得る。従って S = πr2 である。
脚注
注釈
- ^ 同様の計算は問題41の円筒の体積を求める際にも行われている。
- ^ 著者であるアーメスは
 の例を計算している。この場合、結果は整数となる。
の例を計算している。この場合、結果は整数となる。 - ^ 実際には、円周を
 、直径を
、直径を  とすると、
とすると、 であることを示した。
であることを示した。 - ^ この方法は、二重帰謬法、二重背理法とも呼ばれる。
- ^ 実際には半径1尺の円を用いており、1尺=10寸であるが単位は略した。
- ^ 小学校学習指導要領において具体的な教示法は示されていないものの、その解説において「円の変形による式の導出」として、円をいくつかの扇形に分割し長方形に近似させる方法が掲げられている[25]
- ^ これは例えば『岩波講座 現代数学への入門』、『理工系の微積分入門』による方法を四分円に適用したもの。
- ^ 『数学公式II』では、
 の極限値として
の極限値として が示されている。
が示されている。 である。
である。
出典
- ^ 伊東俊太郎編, 数学の歴史 2『中世の数学』共立出版, 1987年
- ^ 小学校学習指導要領(平成 29 年告示)解説 算数編 平成 29年7月 文部科学省 pp.297-298
- ^ 文部科学省 (2018年). “高等学校学習指導要領(平成30年告示)”. 文部科学省. 2021年11月22日時点のオリジナルよりアーカイブ。2022年3月13日閲覧。
- ^ 山川, 宏史「円の面積 S = πr2 の循環論法の解消について」(pdf)『数研通信』第58巻、2007年、9–11。
- ^ 関口晃司『円の面積をめぐる循環論法からの脱却のために』(PDF)高知工科大学、2014年。 オリジナルの2021年7月11日時点におけるアーカイブ。https://web.archive.org/web/20210711183021/http://www.core.kochi-tech.ac.jp/m_inoue/work/pdf/sekiguti/highschool/2.pdf。2022年3月13日閲覧。
参考文献
- 矢野健太郎 編『数学小辞典』(第2版増補)共立出版、2017年5月。ISBN 978-4-320-11319-0。
- 中村滋、室井和男『数学史 数学5000年の歩み』共立出版、2014年11月。ISBN 978-4-320-11095-3。
- Delahaye, Jean‐Paul 著、畑政義 訳『π ― 魅惑の数』朝倉書店、2001年9月。ISBN 978-4-254-11086-9。
- 日本数学史学会 編『数学史事典』丸善、2020年10月。ISBN 978-4-621-30522-5。
- 日本数学会 編『岩波数学辞典』(第4版)岩波書店、2007年3月。ISBN 978-4-000-80309-0。
- 上垣渉『はじめて読む数学の歴史』角川学芸出版〈角川ソフィア文庫〉、2016年8月25日。ISBN 978-4-044-00143-8。
- 安部齊『微積分の歩んだ道』森北出版、1989年6月。ISBN 978-4-627-01710-8。
- 上野健爾『円周率が歩んだ道』岩波書店〈岩波現代全書〉、2013年6月18日。ISBN 978-4-000-29104-0。
- アルキメデス, 『方法』
- アルキメデス 著、佐藤徹 訳『アルキメデス方法』東海大学出版〈東海大学古典叢書〉、1990年2月。ISBN 4-486-01102-3。
- 和算研究所 編『和算百科』丸善出版、2017年10月10日。ISBN 978-4-621-30174-6。
- 佐藤健一 編『『塵劫記』初版本』研成社、2006年4月20日。ISBN 4-87639-409-1。
- Posamentier, Alfred S.、Lehmann, Ingmar 著、松浦俊輔 訳『不思議な数πの伝記』日経BP社、2005年11月。ISBN 4-8222-8245-7。
- 中川仁 (2008年9月3日). “円周率πを計算する ―アルキメデス,和算,ガウスの方法―”. juen.ac.jp. 2022年2月22日閲覧。
- 中村, 正明「アルキメデスの方法によるπの計算」『日本数学教育学会誌』第58巻第5号、1976年、83–91、doi:10.32296/jjsme.58.5_5、ISSN 0021-471X。
- 斎藤憲『よみがえる天才アルキメデス』岩波書店、2006年。
- Boyer, Carl B. 著、加賀美鐵雄・浦野由有 訳『数学の歴史 2』朝倉書店、1984年。
- 平山諦『円周率の歴史』中教出版、1955年8月。ISBN 978-4-044-00143-8。
- 阪井章『理工系の微積分入門』共立出版、2001年10月。ISBN 4-320-01665-3。
- I.N.Bronstein、K.A.Semendjajew『数学ハンドブック』矢野健太郎監・宮本敏雄訳、森北出版、1985年11月。ISBN 4-627-05080-1。
- 飯高茂・楠岡成雄・室田一雄 編『朝倉数学ハンドブック [基礎編]』朝倉書店、2010年5月。ISBN 978-4-254-11123-1。
- 青木和彦『微分と積分 1』岩波書店〈岩波講座 現代数学への入門〉、1995年。ISBN 4-00-010621-X。
- 森口繁一、宇田川銈久、一松信『数学公式II』岩波書店〈岩波全書 229〉、1957年。doi:10.11501/1373779。
- 武藤徹『面積の発見』岩波書店〈岩波科学ライブラリー 200〉、2012年12月。ISBN 978-4-00-029600-7。




































































![{\displaystyle {\begin{aligned}S_{4}&=\int _{0}^{r}{\sqrt {r^{2}-x^{2}}}\,dx\\&=\left[{\frac {1}{2}}(x{\sqrt {r^{2}-x^{2}}}+r^{2}\arcsin {\frac {x}{r}})\right]_{0}^{r}\\&={\frac {\pi r^{2}}{4}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75c9bfd2798b812d28a0fce06c0ba92da4585f05)







![{\displaystyle {\begin{aligned}S_{4}&=\int _{0}^{\frac {\pi }{2}}r^{2}\cos ^{2}t\,dt\\&=r^{2}\int _{0}^{\frac {\pi }{2}}{\frac {1+\cos 2t}{2}}\,dt\\&={\frac {r^{2}}{2}}\left[t+{\frac {\sin 2t}{2}}\right]_{0}^{\frac {\pi }{2}}\\&={\frac {\pi r^{2}}{4}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12a359b57d4f1b1fe4898a8c008e66eac8c06ad4)

![{\displaystyle [0,r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e37e877243c4e605346083360f52c6faea13009e)



![{\displaystyle [x_{k-1},x_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f77539e232b976d1a83e1829624235bba4164757)











![{\displaystyle {\begin{aligned}S=\int _{0}^{r}\,dS&=\int _{0}^{r}2\pi x\,dx\\&=2\pi \left[{\frac {x^{2}}{2}}\right]_{0}^{r}\\&=\pi r^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c8c2c2489681c9c3719c546c339c73839d915b7)










