Linea spettrale atomica

In fisica, le linee spettrali atomiche sono di due tipi:

• Una linea di emissione si forma quando in atomo un elettrone compie una transizione da un particolare livello energetico discreto a uno stato energetico inferiore, emettendo un fotone con una particolare energia e lunghezza d'onda. Uno spettro di molti di tali fotoni mostrerà un picco di emissione nella lunghezza d'onda ad essi associata.
• Una linea di assorbimento si forma quando un elettrone compie una transizione da uno stato di energia discreta inferiore a uno superiore, nel cui processo viene assorbito un fotone. Questi fotoni assorbiti in genere provengono da una radiazione continua di fondo e lo spettro mostrerà un calo della radiazione continua nella lunghezza d'onda associata ai fotoni assorbiti.

I due stati devono essere stati legati nei quali l'elettrone viene confinato nell'atomo, in modo che la transizione viene a volte indicata come transizione "legato-legato" (bound-bound), a differenza della transizione in cui l'elettrone viene espulso completamente fuori dall'atomo (transizione "legato-libero" (bound-free)), in una condizione in cui gli stati non hanno energie discrete, ma continue, lasciando l'atomo ionizzato e generando uno spettro continuo, senza linee ben definite.

Durante il processo viene emesso o assorbito un fotone con un'energia uguale alla differenza di energia tra i livelli. La frequenza ${\displaystyle \nu }$ in cui si trova la linea spettrale è correlata all'energia del fotone ${\displaystyle E}$ tramite la legge di Planck ${\displaystyle E=h\nu }$ dove ${\displaystyle h}$ è la costante di Planck.

Coefficienti di emissione e di assorbimento

L'emissione di radiazioni di linea atomica può essere descritta da un coefficiente di emissione ${\displaystyle \epsilon }$ con unità di energia/tempo/volume/angolo solido. Con ε dt dV dΩ viene dunque indicata l'energia emessa da un elemento di volume ${\displaystyle dV}$ nel tempo ${\displaystyle dt}$ dentro un angolo solido ${\displaystyle d\Omega }$. Per la radiazione della linea atomica:

${\displaystyle \epsilon ={\frac {h\nu }{4\pi }}n_{2}A_{21}}$

dove ${\displaystyle n_{2}}$ è la densità di atomi emittenti, ${\displaystyle A_{21}}$ è il coefficiente di Einstein per l'emissione spontanea, la quale viene fisata per ogni due livelli di energia. Per la legge di Kirchhoff, le caratteristiche dell'assorbimento in una regione di spazio sono strettamente legate alle sue emissioni caratteristiche, così dobbiamo menzionare anche il coefficiente di assorbimento ${\displaystyle \kappa }$ che avrà unità di 1/lunghezza e κ' dx fornisce la frazione di intensità assorbita da un raggio di luce alla frequenza ν mentre percorre la distanza dx. Il coefficiente di assorbimento è dato da:

${\displaystyle \kappa '={\frac {h\nu }{4\pi }}~(n_{1}B_{12}-n_{2}B_{21})}$

dove ${\displaystyle I_{\nu }}$ è l'intensità spettrale di radiazione alla (e vicino alla) frequenza ${\displaystyle \nu }$; ${\displaystyle n_{1}}$ è la densità degli atomi assorbenti, e ${\displaystyle B_{12}}$ e ${\displaystyle B_{21}}$ sono rispettivamente i coefficienti di Einstein per l'assorbimento e l'emissione indotta. Similmente al coefficiente ${\displaystyle A_{21}}$, questi sono anche costanti per ognuno dei due livelli energetici.

Nel caso di equilibrio termodinamico locale, le densità degli atomi, sia eccitati che non eccitati, possono essere calcolate dalla distribuzione di Maxwell-Boltzmann, ma per altri casi, (per es. i laser) il calcolo è più complicato.

L'equazione precedente ha ignorato l'influenza della forma della linea spettrale. Per essere precisi, le equazioni di cui sopra devono essere moltiplicate per la forma della linea spettrale (normalizzata), nel qual caso le unità cambieranno per includere un termine di 1/Hz.

I coefficienti di Einstein

Nel 1916, Albert Einstein ha suggerito che vi siano essenzialmente tre processi che si verificano nella formazione di una linea spettrale atomica: emissione spontanea, emissione stimolata e assorbimento. A ciascuno di essi è associato un coefficiente di Einstein il quale misura la probabilità con cui quel particolare processo accade.

Emissione spontanea

L'emissione spontanea è il processo mediante il quale un elettrone "spontaneamente" (vale a dire senza nessuna influenza esterna) decade da un livello energetico superiore a uno più basso. Il processo è descritto dal coefficiente di Einstein ${\displaystyle A_{21}}$ (s^-1) il quale dà la probabilità per l'unità di tempo in cui un elettrone nello stato 2 con energia ${\displaystyle E_{2}}$ decadrà spontaneamente allo stato 1 con energia ${\displaystyle E_{1}}$, emettendo un fotone con un'energia ${\displaystyle E_{2}-E_{1}=h\nu }$. A causa dell'principio di incertezza di energia-tempo, la transizione produce effettivamente fotoni con un ristretto campo di frequenze chiamate larghezza di linea spettrale. Se ${\displaystyle n_{i}}$ è la densità del numero di atomi in stato i  allora il mutamento nella densità del numero di atomi in stato 1 per unità di tempo dovuto all'emissione spontanea sarà:

${\displaystyle \left({\frac {dn_{1}}{dt}}\right)_{A_{21}}=A_{21}n_{2}}$

Emissione stimolata

L'emissione stimolata (nota anche come emissione indotta) è il processo mediante il quale un elettrone è indotto a saltare da un livello energetico più alto a uno inferiore per la presenza di radiazione elettromagnetica alla (o quasi alla) frequenza della transizione. Il processo viene descritto dal coefficiente di Einstein ${\displaystyle B_{21}}$ (sr·m²·Hz·W^-1·s^-1 = sr·m²·J^-1·s^-1), il quale dà la probabilità per mezzo dell'unità di tempo per unità di radianza spettrale del campo di radiazione che un elettrone nello stato 2 con energia ${\displaystyle E_{2}}$ decadrà allo stato 1 con energia ${\displaystyle E_{1}}$, emettendo un fotone con un'energia ${\displaystyle E_{2}-E_{1}=h\nu }$. Il cambiamento della densità del numero di atomi nello stato 1 per unità di tempo dovuto a emissioni indotte sarà:

${\displaystyle \left({\frac {dn_{1}}{dt}}\right)_{B_{21}}=B_{21}n_{2}\rho (\nu );\quad \quad \rho (\nu )={\frac {2h\nu ^{3}}{c^{2}(e^{h\nu /kT}-1)}}}$

dove ${\displaystyle \rho (\nu )}$ è la densità di radiazione del campo della radiazione alla frequenza della transizione (vedi legge di Planck).

L'emissione stimolata è uno dei processi fondamentali che conducono allo sviluppo del laser.

Foto-assorbimento

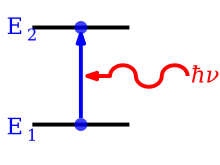
L'assorbimento è il processo mediante il quale un fotone viene assorbito dall'atomo, facendo passare un elettrone da un livello energetico inferiore a uno superiore. Il processo è descritto dal coefficiente di Einstein ${\displaystyle B_{12}}$ (sr·m²·Hz·W^-1·s^-1 = sr·m²·J^-1·s^-1), il quale fornisce la probabilità per mezzo dell'unità di tempo per unità di radianza spettrale del campo di radiazione dove un elettrone nello stato 1 con energia ${\displaystyle E_{1}}$ assorbirà un fotone con un'energia ${\displaystyle E_{2}-E_{1}=h\nu }$ saltando allo stato 2 con un'energia ${\displaystyle E_{2}}$. Il mutamento della densità del numero di atomi nello stato 1 per unità di tempo dovuto all'assorbimento sarà:

${\displaystyle \left({\frac {dn_{1}}{dt}}\right)_{B_{12}}=-B_{12}n_{1}\rho (\nu )}$

Bilanciamento dettagliato

I coefficienti di Einstein sono probabilità fisse associate ad ogni atomo e non dipendono dallo stato del gas di cui gli atomi fanno parte. Perciò, ogni rapporto che si può ricavare tra i coefficienti, diciamo, in equilibrio termico sarà valido universalmente.

Nell'equilibrio avremo un semplice bilanciamento in cui la variazione netta del numero di ogni atomo eccitato è zero, essendo bilanciato dalla perdita e dal guadagno causati da tutti i processi. Per quanto riguarda le transizioni "legate al confine", avremo anche bilanciamento dettagliato, il quale stabilisce che il netto scambio tra ognuno dei due livelli sarà in equilibrio. Questo succede perché la probabilità di transizione non può essere influenzata dalla presenza o assenza di altri atomi eccitati. L'equilibrio dettagliato (valido solo in condizioni di equilibrio) richiede che il cambiamento nel tempo del numero di atomi nel livello 1 a causa dei tre processi precedenti sia pari a zero:

${\displaystyle 0=A_{21}n_{2}+B_{21}n_{2}I(\nu )-B_{12}n_{1}I(\nu )}$

Insieme al bilanciamento dettagliato, possiamo usare la nostra conoscenza della distribuzione di energia in equilibrio degli atomi, come stabilito nella distribuzione di Maxwell-Boltzmann e la distribuzione di equilibrio dei fotoni, come stabilito nella legge di Planck della radiazione del corpo nero per derivare rapporti universali tra i coefficienti di Einstein

Dalla distribuzione di Maxwell-Boltzmann abbiamo per il numero di specie di atomi eccitati i:

${\displaystyle {\frac {n_{i}}{n}}={\frac {g_{i}e^{-E_{i}/kT}}{Z}}}$

dove n è la densità totale della specie atomica, eccitata e non eccitata, k è la costante di Boltzmann, T è la temperatura, ${\displaystyle g_{i}}$ è la degenerazione di stato i, e Z è la funzione di partizione. Dalla legge di Planck sulla radiazione del corpo nero abbiamo per la radianza spettrale alla frequenza ${\displaystyle \nu }$

${\displaystyle I(\nu )={\frac {F(\nu )}{e^{h\nu /kT}-1}}}$

dove:

${\displaystyle F(\nu )={\frac {2h\nu ^{3}}{c^{2}}}}$

dove ${\displaystyle c}$ è la velocità della luce e ${\displaystyle h}$ è la costante di Planck. Da notare che in alcuni trattamenti, viene utilizzata la densità di energia del corpo nero piuttosto che la radianza spettrale, nel qual caso:

${\displaystyle F(\nu )={\frac {8\pi \hbar \nu ^{3}}{c^{3}}}}$

Sostituendo queste espressioni nell'equazione del bilanciamento dettagliato e ricordando che ${\displaystyle E_{2}-E_{1}=h\nu }$ si ottiene:

${\displaystyle A_{21}g_{2}e^{-h\nu /kT}+B_{21}g_{2}e^{-h\nu /kT}{\frac {F(\nu )}{e^{h\nu /kT}-1}}=B_{12}g_{1}{\frac {F(\nu )}{e^{h\nu /kT}-1}}}$

L'equazione precedente deve reggere a qualsiasi temperatura, in modo che i tre coefficienti di Einstein siano correlati da:

${\displaystyle {\frac {A_{21}}{B_{21}}}=F(\nu )}$

e

${\displaystyle {\frac {B_{21}}{B_{12}}}={\frac {g_{1}}{g_{2}}}}$

Quando questo rapporto è inserito nell'equazione originale, si può anche trovare una relazione tra ${\displaystyle A_{21}}$ e ${\displaystyle B_{12}}$, che coinvolga la legge di Planck.

Forze dell'oscillatore

La forza dell'oscillatore ${\displaystyle f_{12}}$ viene definita per mezzo della seguente relazione per la sezione d'urto (cross section) ${\displaystyle a_{12}}$ per assorbimento:

${\displaystyle a_{12}={\frac {\pi e^{2}}{m_{e}c}}\,f_{12}}$

dove ${\displaystyle e}$ è la carica dell'elettrone e ${\displaystyle m_{e}}$ è la massa dell'elettrone. Questo permette a tutti e tre i coefficienti di Einstein di essere espressi in termini della singola forza dell'oscillatore associata alla particolare linea spettrale atomica:

${\displaystyle B_{12}={\frac {4\pi ^{2}e^{2}}{m_{e}h\nu c}}\,f_{12}}$

${\displaystyle B_{21}={\frac {4\pi ^{2}e^{2}}{m_{e}h\nu c}}~{\frac {g_{1}}{g_{2}}}~f_{12}}$

${\displaystyle A_{21}={\frac {8\nu ^{2}\pi ^{2}e^{2}}{m_{e}c^{3}}}~{\frac {g_{1}}{g_{2}}}~f_{12}}$

Bibliografia

• (EN) S. Chandrasekhar, Radiative Transfer, Dover Publications, Inc. New York, 1960, ISBN 0-486-60590-6.
• (EN) E.U. Condon, G.H. Shortley, The Theory of Atomic Spectra, Cambridge University Press, 1964, ISBN 0-521-09209-4.
• (EN) G.B. Rybicki, A.P. Lightman, Radiative processes in Astrophysics, John Wiley & Sons, New York, 1985, ISBN 0-471-82759-2.
• (EN) F.H. Shu, The Physics of Astrophysics - Volume 1 - Radiation, University Science Books, Mill Valley, CA, 1991, ISBN 0-935702-64-4.
• (EN) Robert C. Hilborn, Einstein coefficients, cross sections, f values, dipole moments, and all that, in Am. J. Phys. 50, 982, 1982.

Voci correlate

• Configurazione elettronica
• Spettroscopia atomica
• Distribuzione di Breit-Wigner
• Spettroscopia di emissione, spettri continui emessi dalle molecole

Altri progetti

• Wikimedia Commons contiene immagini o altri file su Linea spettrale atomica